And we're done! Thanks for a great semester!
- All final exams have been graded. Graded exams are available on Gradescope.
- Regrade requests for the final exam may be submitted on Gradescope through January 20, 2023, the first Friday of the Spring 2023 semester. We reserve the right to ignore regrade requests whose positive outcome would not increase any course grade, and we are unlikely to answer any regrade requests before January 10.
- Course grades have been submitted to Banner. Grades should be visible in your academic history by Friday, December 23. Course grades were computed as described in the grading policies, using the advertised fixed cutoffs, with the following adjustments:
- All regrade requests submitted before the final exam were answered and closed.
- For purposes of computing homework averages, homework scores less than or equal to 4/10 (beyond the minimum 16) were dropped.
- The exam is cumulative; it will cover the same material as Homeworks 0 through 9. The exam will also assume familiarity with relevant prerequisite material, especially basic graph algorithms, but the main emphasis will be on material from this course.
- There will be a conflict exam for students who cannot take the regular exam for any of the reasons outlined in the student code. The exact time of the conflict exam will depend on the final exam schedules of students ho need to take it. Watch this page for a link to a registration page.
- Instead of the regular lecture, there will be an optional review session today; Jeff will walk through a sample exam.
- Please read and understand the exam policies. In particular, you are allowed to being two double-sided cheat sheets to the exam, which must be hand-written.
- Lots of study materials are available:
- Jeff's textbook and notes, especially chapters/notes linked from the schedule page.
- Jeff's past CS 473 exams can be found in his course materials archive. (Topical coverage varies from semester to semester; you can safely ignore past exam questions on material we have not covered.)
- Other useful resources, including lecture notes, lecture videos, slides, homeworks, exams, and other course materials from other CS 473 instructors and from comparable algorithms courses elsewhere.
- Once again, there will be no question 3.
- Solutions for Homework 9 are available.
- "Homework 10" is available. This is a small collection of practice problems, some of which draw on material from earlier in the course. We will release solutions on Monday, December 5.
- Regrade requests can be submitted directly on Gradescope until Friday, December 16.
- Here is a distribution of midterm scores and predicted course grades so far.
- For each student, we computed an overall average = 30% Homeworks 0–7 (with lowest 6 scores dropped) + 70% Midterm 1. The orange curve shows these overall averages in sorted order. Those averages were used to compute the vertical letter-grade boundaries, following the advertised fixed cutoffs.
- The blue dots show the corresponding midterm scores for each student. Dots further above the orange curve indicate students with lower homework averages. Note that the two plots are on different scales.

- Here is a scatterplot of Midterm 1 scores versus midterm 2 scores, with letter-grad cutoffs assuming a 90% homework average.
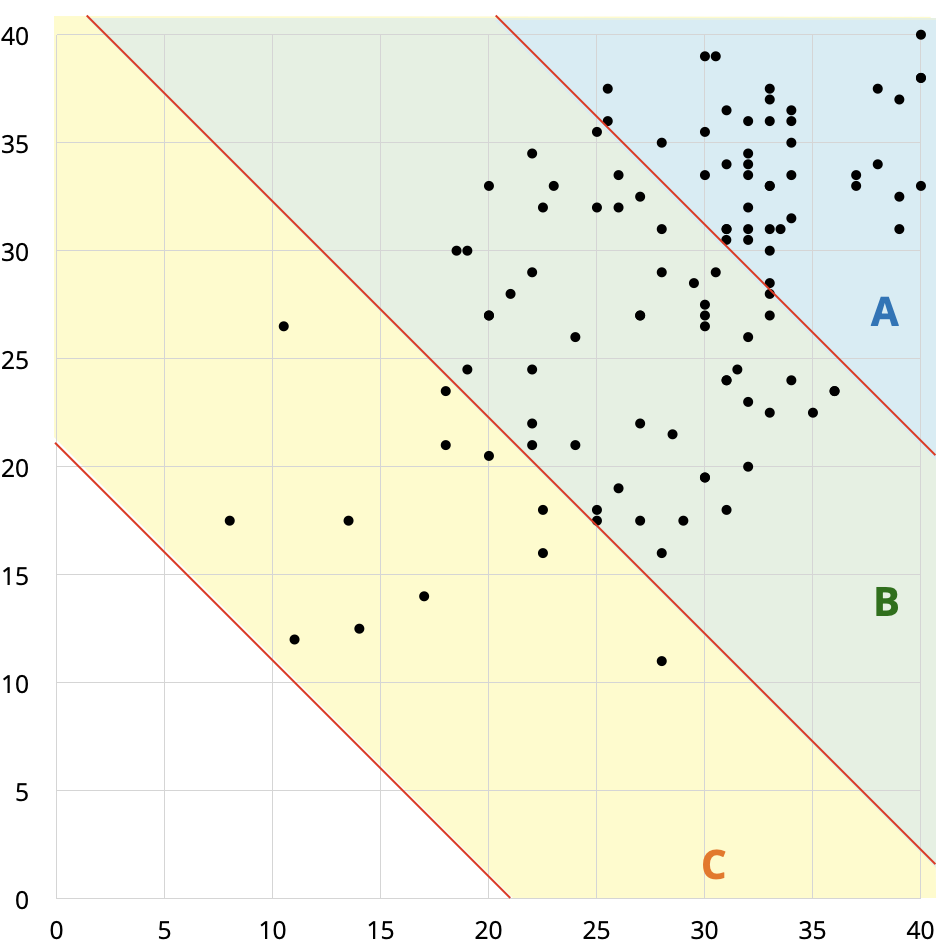
- At least for now, there is no curve. As with Midterm 1, the overall score distibution for Midterm 2 is slightly higher than in past (pre-pandemic) semesters of CS 473. Thus, we expect to use the advertised fixed cutoffs to compute course grades.
Assuming a homework average of 90% (the class median), a total midterm score of 63 or higher is consistent with an A in the course, a total midterm score between 42 and 62 is consistent with a B, and a midterm score between 22 and 42 is consistent with a C.
- Please keep in mind that this is only a rough prediction of your final course grades, based on less than a third of the overall work. Past experience suggests that most students‘ final course grades will be within half a letter grade of these estimates, but there are a few differences of a letter grades or more (in either directions) every semester.
- The exam will cover the same material as Homeworks 4, 5, 6, and 7: discrete probability, randomized algorithms, hashing, string matching, and maximum flows/minimum cuts, including material from today's lecture. The exam will assume familiarity with relevant prerequisite material, especially basic graph algorithms, but the main emphasis will be on material from this course.
- There will be a conflict exam on Tuesday, November 1, for students who cannot take the regular exam for any of the reasons outlined in the student code. To register for the conflict exam, please fill out this form by Friday, October 28.
- Instead of the regular lecture, there will be an optional review session on Thursday, October 27; Jeff will walk through a sample exam.
- Please read and understand the exam policies. In particular, you are allowed to being one double-sided handwritten cheat sheet to the exam.
- Lots of study materials are available:
- Jeff's textbook and notes, especially chapters/notes linked from the schedule page.
- Jeff's past CS 473 exams can be found in his course materials archive. (Topical coverage varies from semester to semester; you can safely ignore past midterm questions on material we have not covered.)
- Other useful resources, including lecture notes, lecture videos, slides, homeworks, exams, and other course materials from other CS 473 instructors and from comparable algorithms courses elsewhere.
- There will be no question 3.
- Regrade requests can be submitted directly on Gradescope until Monday, October 23.
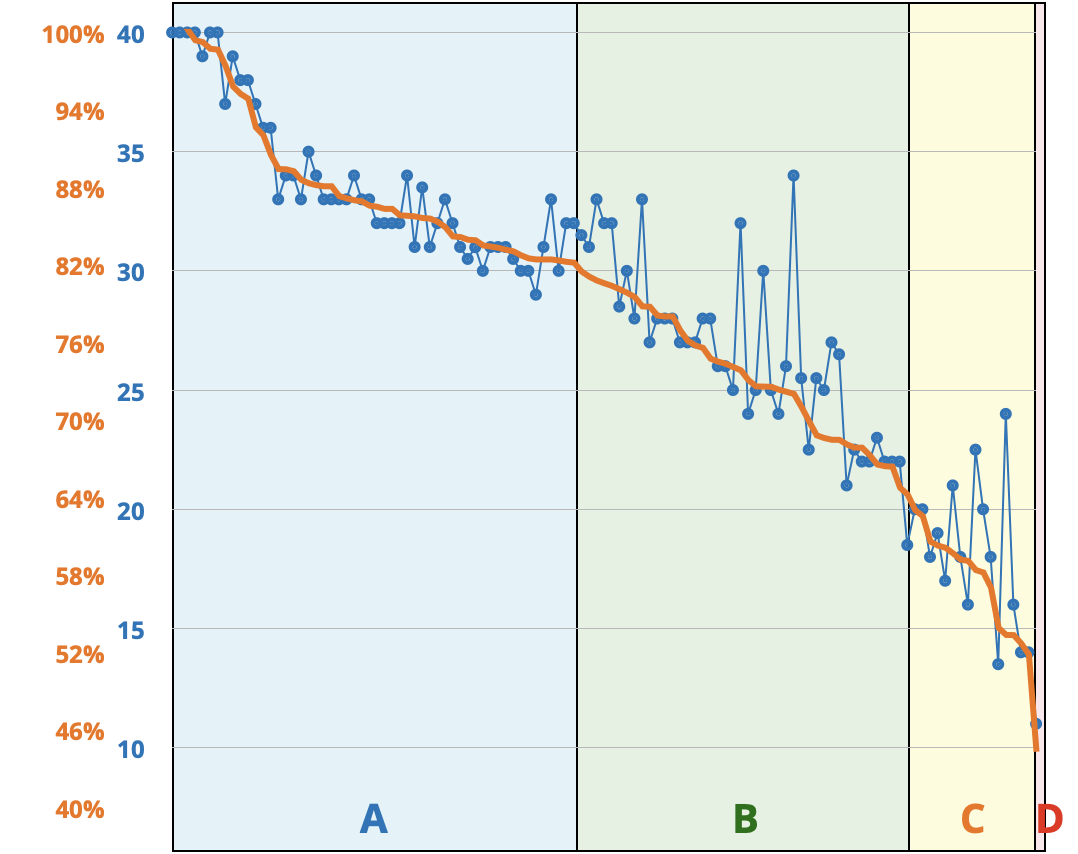
- Here is a distribution of midterm scores and predicted course grades so far.
- For each student, we computed an overall average = 30% Homeworks 0–3 (with lowest 3 scores dropped) + 70% Midterm 1. The orange curve shows these overall averages in sorted order, omiyying a small handful of students with averages below 40%. Those averages were used to compute the vertical letter-grade boundaries, following the advertised fixed cutoffs.
- The blue dots show the corresponding midterm scores for each student. Dots further above the orange curve indicate students with lower homework averages. Note that the two plots are on different scales.
- At least for now, there is no curve. Despite lower average scores on problem 3, the overall score distibution for Midterm 1 is slightly higher than in past (pre-pandemic) semesters of CS 473. Thus, we expect to use the advertised fixed cutoffs to compute course grades.
Assuming a homework average of 96% (the class median), a midterm score between 30 and 40 is consistent with an A in the course, a midterm score between 20 and 30 is consistent with a B, and a midterm score between 10 and 20 is consistent with a C.
- Please keep in mind that this is an extremely rough prediction of your final course grades, based on less than a third of the overall work. Past experience suggests that most students‘ final course grades will be within one letter grade of these estimates, but differences of a full letter grade (in either direction) are quite common, and there are a few differences of two letter grades or more (in either directions) every semester.
- Students are strongly encouraged to talk with Jeff before dropping the class. Students who are thinking of dropping the class and/or are seriously concerned about their midterm performance will have priority will have priority over others during Jeff's office hours this week.
- The exam will cover the same material as Homeworks 0, 1, 2, and 3: prerequisite material, divide-and-conquer algorithms, fast Fourier transforms, and dynamic programming. Nothing on the exam will require more advanced dynamic programming techinques (divide-and-conquer optimization, monotonicity, or SMAWK).
- There will be a conflict exam on Tuesday, September 27, for students who cannot take the regular exam for any of the reasons outlined in the student code. To register for the conflict exam, please fill out this form by Friday, September 23.
- Instead of the regular lecture, there will be an optional review session on Thursday, September 22; Jeff will walk through a sample exam.
- Please read and understand the exam policies. In particular, you are allowed to being one double-sided handwritten cheat sheet to the exam.
- Lots of study materials are available:
- Jeff's textbook — especially chapters on backtracking, dynamic programming, and depth-first search (for dynamic programming in dags) — and his lecture notes on FFTs
- Jeff's past CS 473 exams can be found in his course materials archive. (Topical coverage varies from semester to semester; you can safely ignore past 473 Midterm 1 questions on approximation algorithms or randomization.)
- Other useful resources, including lecture notes, lecture videos, slides, homeworks, exams, and other course materials from other CS 473 instructors and from comparable algorithms courses elsewhere.
- Homework 3 is due next Tuesday, September 20, at 9pm. This is the last homework before Midterm 1.
- Homework 0 grades have been released on Gradescope.
Starting with this homework, groups of up to three students can submit joint solutions for each problem. For each problem, exactly one member of each group should submit that group's solution and identify the other group members (if any) on Gradescope. Please remember to list all group members at the top of the first page of each submission. Finally, please see the academic integrity policies for group homework.
- Welcome! We're working hard to get everything set up before the semester begins. Meanwhile, you may notice broken links and/or text that refers to previous semesters.
- The first lecture is Tuesday, August 23.
- Homework 0 is due the following Tuesday, August 30 at 9pm. Each student must submit their own individual solutions on Gradescope. A LaTeX template for homework solutions is available.