MP 5 PhotoMosaic
- Monday, March 26 at 11:59 PM 3/26 @ 11:59 PM
- Monday, April 2 at 11:59 PM 4/2 @ 11:59 PM
MP5 is a partner MP!
- Part 1 and Part 2 of this MP can be completed with a partner!
- The creative “Part 3” must be completed by yourself and must be unique (and different from your partner’s work).
You should denote who you work with in the PARTNERS.txt file in mp5. If you worked alone, include only your NetID in PARTNERS.txt.
Goals and Overview
In this MP, you will:
- learn about k-d trees
- implement and use a nearest neighbor search (NNS) algorithm
- practice using templates
- practice
const-correctness - use your knowledge to make a useful application
Videos
- k-d tree : 2-D example
- (partition based) Quick Select
- findNearestNeighbor - Part 1: Explanation
- findNearestNeighbor - Part 2: Walkthrough
Checking Out Your Code
From your CS 225 git directory, run the following on EWS:
git fetch release
git merge release/mp5 -m "Merging initial mp5 files"If you’re on your own machine, you may need to run:
git fetch release
git merge --allow-unrelated-histories release/mp5 -m "Merging initial mp5 files"Upon a successful merge, your MP5 files are now in your mp5 directory.
You can see all of the required functions on the TODO page on the Doxygen for this MP.
A list of relevant files is here.
Background: PhotoMosaics
A PhotoMosaic is a picture created by taking some source picture, dividing it up into rectangular sections, and replacing each section with a small thumbnail image whose color closely approximates the color of the section it replaces. Viewing the PhotoMosaic at low magnification, the individual pixels appear as the source image, while a closer examination reveals that the image is made up of many smaller tile images.
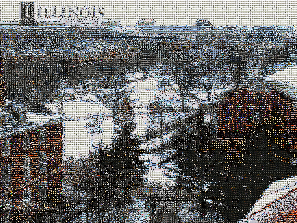
Click for the (rather large) full-size mosaic
For this project you will be implementing parts of a PhotoMosaic generator. Specifically your code will be responsible for deciding how to map tile images to the rectangular sections of pixels in the source image. Selecting the appropriate tile image is supported by a data structure called a $$k$$-d tree which we will describe in the next section. The pool of tile images are specified by a local directory of images. We provide the code to create the TileImage pool and the code to create the mosaic picture from a tiled source image.
Background: K-d trees
Binary Search Trees are linear data structures that support the Dictionary ADT
operations (insert, find, remove). They also support nearest neighbor
search: If you have a binary search tree, given a key that may or may not be in
the tree, you can find the closest key that is in the tree. To do so, you just
recursively walk down the tree, as in find, keeping track of the closest node
found:
K BST<K,V>::findNearestNeighbor(Node * croot, K target)
{
// Look in the left or right subtree depending on whether target is smaller or larger than our current root
if (target < croot->key)
{
// if we have no child in the correct direction, our root must be the closest
if (croot->left == NULL)
return croot->key;
childResult = findNearestNeighbor(croot->left);
}
else
{
if (croot->right == NULL)
return croot->key;
childResult = findNearestNeighbor(croot->right);
}
// Calculate closest descendent node's distance to the target
childDistance = distance(childResult, target);
// Find the distance of this node to the target
currDistance = distance(croot->key, target);
// If the root node is closer, return it, otherwise return the closer child
if (currDistance < childDistance)
return croot->key;
else
return childResult;
}A $$k$$-d tree is a generalization of a Binary Search Tree that supports nearest neighbor search in higher numbers of dimensions — for example, with 2-D or 3-D points, instead of only 1-D keys. A 1-D-tree (a $$k$$-d tree with $$k = 1$$) is simply a binary search tree. For this MP, you will be creating a photomosaic, which requires that given a region on our original image, we can determine which of our available images best fills that region. If we use the average color of regions and tile-images, this can be determined by finding the nearest colored tile image to a given region. If we treat colors as $$(H, S, L)$$ points in 3-D space, we can solve this problem with a 3-D tree.
More formally, a $$k$$-d tree is special purpose data structure used to organize elements that can be described by locations in $$k$$-dimensional space. It is considered a space-partitioning data structure because it recursively subdivides a space into two convex sets. These sets are rectangular regions of the space called hyperrectangles. $$k$$-d trees are particularly useful for implementing nearest neighbor search, which is an optimization problem for finding the closest element in $$k$$-dimensional space.
A $$k$$-d tree is a rooted binary tree. Each node in the tree represents a point in $$k$$-d-space, as well as a line (hyperplane) defined by one dimension of this point, which divides this space into two regions (hyperrectangles). At each level in the tree, a different dimension is used to decide the direction of the splitting line (hyperplane). An element is selected to define the splitting line by its coordinate value for the current dimension. This element should be the median of all the points in this part of the tree, taken over the current dimension. A node is then created for this element in the tree and its children are created recursively using the same process, which repeats until no elements remain in the region (hyperrectangle). The splitting dimension at any level of the tree can be selected to find the best partition of the data. For our purposes, we will change dimension cyclically, in order (for $$k = 3$$, we will use dimensions $$0, 1, 2, 0, 1, 2, 0, \ldots$$).
Figure 1: the tree on the left is an example 2-dimensional $$k$$-d tree and the diagram on the right shows how the space is partitioned by the splitting planes into hyperrectangles for that tree. (Note that our implementation will make a slightly different tree from this set of points because of the way we will define the median.)
$$k$$-d trees are particularly useful for searching points in Euclidean space. Perhaps the most common use of a $$k$$-d tree is to allow for fast search for the nearest neighbor of a query point, among the points in the tree. That is, given an arbitrary point in $$k$$-dimensional space, find the point in the tree which is nearest to this point. The search algorithm is defined in detail below.
For this MP, we will be using a 3-D tree (a 3-dimensional $$k$$-d tree) to find
the closest average color of TileImages to the average color of pixel
sections in the source image. With the pool of average colors organized in a
$$k$$-d tree, we can search for the best tile to match the average color of
every region in the input image, and use it to create a PhotoMosaic!
Requirements
These are strict requirements that apply to both parts of the MP. Failure to follow these requirements may result in a failing grade on the MP.
- You are required to comment the MP as per the commenting standard described by the Coding Style Policy.
- You must name all files, public functions, public member variables (if any exist), and executables exactly as we specify in this document.
- Your code must produce the exact output that we specify: nothing more, nothing less. Output includes standard and error output and files such as images.
- Your code must compile on the EWS machines using clang++. Being able to compile on a different machine is not sufficient.
- Your code must be submitted correctly by the due date and time. Late work is not accepted.
- Your code must not have any memory errors or leaks for full credit. Valgrind tests will be performed separately from the functionality tests.
- Your public function signatures must match ours exactly for full credit.
If using different signatures prevents compilation, you will receive a zero.
Tests for
const-correctness may be performed separately from the other tests (if applicable).
Assignment Description
We have provided the bulk of the code to support the generation of
PhotoMosaics. There is one critical component that is missing: the
KDTileMapper. This class is responsible for deciding which TileImages to
use for each region of the original image. In order to make this decision it
must be able to figure out which TileImage has the closest average color to
the average color of that region. A data structure called a $$k$$-d tree is
used to find the nearest neighbor of a point in $$k$$-dimensional space.
This assignment is broken up into the following two parts:
As usual, we recommend implementing, compiling, and testing the functions in MP 5.1 before starting MP 5.2.
MP 5.1
For the first part of MP 5, you will implement a generic KDTree class that
can be used to organize points in $$k$$-dimensional space, for any integer $$k
> 0$$.
The KDTree class
Although we will only be using a 3-D tree, we want you to create a more general data structure that will work with any positive non-zero number of dimensions. Therefore, you will be creating a templated class where the template parameter is an integer, specifying the number of dimensions. We have provided the skeleton of this class, but it is your assignment to implement the member functions and any helper functions you need.
A $$k$$-d tree is constructed with Points in $$k$$-dimensional space. To
support this, we have provided a templated Point class, which takes the same
integer template parameter as the $$k$$-d tree.
In this part of assignment we ask you to implement all of the following member functions.
Implementing smallerDimVal
Please see the Doxygen for smallerDimVal.
This function should take in two templatized Points and a dimension and
return a boolean value representing whether or not the first Point has a
smaller value than the second in the dimension specified. That is, if the
dimension passed in is $$k$$, then this should be true if the coordinate of
the first point at $$k$$ is less than the coordinate of the second point at
$$k$$. If there is a tie, break it using Point’s operator<. For
example:
Point<3> a(1, 2, 3);
Point<3> b(3, 2, 1);
cout << smallerDimVal(a, b, 0) << endl; // should print true,
// since 1 < 3
cout << smallerDimVal(a, b, 2) << endl; // should print false,
// since 3 > 1
cout << smallerDimVal(a, b, 1) << endl; // should print true,
// since a < b according to operator<,Implementing shouldReplace
Please see the Doxygen for shouldReplace.
This function should take three templated Points: target, currentBest,
and potential. This should return true if potential is closer (i.e., has
a smaller distance) to target than currentBest (with a tie being broken by
the operator< in the Point class: potential < currentBest). The Euclidean
distance between two $$k$$-dimensional points, $$P(p_1, p_2, \ldots, p_k)$$
and $$Q(q_1, q_2, \ldots, q_k)$$, is the square root of the sum of squares
of the differences in each dimension:
Note that minimizing the distance is the same as minimizing squared-distance, so you can avoid invoking the square root, and just compare squared distances throughout your code:
Point<3> target (1, 3, 5);
Point<3> currentBest1 (1, 3, 2);
Point<3> possibleBest1 (2, 4, 4);
Point<3> currentBest2 (1, 3, 6);
Point<3> possibleBest2 (2, 4, 4);
Point<3> currentBest3 (0, 2, 4);
Point<3> possibleBest3 (2, 4, 6);
cout << shouldReplace(target, currentBest1, possibleBest1) << endl; // should print true
cout << shouldReplace(target, currentBest2, possibleBest2) << endl; // should print false
cout << shouldReplace(target, currentBest3, possibleBest3) << endl; // based on operator<, this should be false!!!Implementing the KDTree Constructor
Please see the Doxygen for the KDTree constructor.
This takes a single parameter, a reference to a constant std::vector of
Point<Dim>s. The constructor should build the tree using recursive helper
function(s).
Just like there is a way to represent a balanced binary search tree using a
specially sorted vector of numbers (how?), we can specially sort a vector of
points in such a way that it represents a $$k$$-d tree. More specifically, in
the KDTree constructor, we are interested in first copying the input list of points
into a points vector, sorting this vector so it represents a $$k$$-d
tree, and building the actual $$k$$-d tree along while we sort.
A rooted binary tree $$T$$ is a $$k$$-d tree if:
- $$T$$ is empty, OR
$$T$$ consists of
- A $$k$$-dimensional point $$r$$ that represents the root of the tree.
- A splitting dimension $$d$$
- Two $$k$$-d tree subtrees $$T_L$$ and $$T_R$$ of splitting dimension
$$(d+1) \bmod k$$ such that
- if $$v$$ is an element in $$T_L$$, then $$v_d \le r_d$$
- if $$v$$ is an element in $$T_R$$, then $$v_d \ge r_d$$
where $$v_d$$ and $$r_d$$ are the $$d$$th components of the points $$v$$ and $$r$$. This property of $$k$$-d trees is called its recursive property because, similar to binary search trees, $$k$$-d trees are recursive data structures.
Furthermore, in our implementation, $$r$$ is the median of all the points (defined below) in $$T$$ in dimension $$d$$.
We define the median of the points across a splitting dimension $$d$$ to be the $$\left\lceil\frac{n}{2}\right\rceil$$ smallest element in a sorted list using $$d$$; in other words, it is the middle-most element of a (odd length) sorted list containing $$n$$ elements. For the general case of the median of a vector between zero-based indices $$a$$ and $$b$$, the median would be the element located at $$\left\lfloor\frac{a+b}{2}\right\rfloor$$.
The median index of $$n$$ nodes is calculated as the cell
$$\left\lfloor\frac{n-1}{2}\right\rfloor$$. That is, the middle index is
selected if there are an odd number of items, and the item before the middle if
there are an even number of items. If there are ties (two points have equal
value along a dimension), they must be decided using the Point class’s
operator<. Although this is arbitrary and doesn’t affect the functionality
of the $$k$$-d tree, it is required to be able to grade your code.
The $$k$$-d tree construction algorithm is defined recursively as follows for a vector of points between indices $$a$$ and $$b$$ at splitting dimension $$d$$:
- Find the median of points with respect to dimension $$d$$.
- Place the median point $$r$$ at index $$m =
\left\lfloor\frac{a+b}{2}\right\rfloor$$ such that
- if point $$v$$ is between indices $$a$$ and $$m-1$$, then $$v_d \leq r_d$$
- if point $$v$$ is between indices $$m+1$$ and $$b$$, then $$v_d \geq r_d$$
- Create a subroot based on the median and then recurse on the indices between $$a$$ though $$m-1$$ for its left subtree, and $$m+1$$ through $$b$$ for its right subtree, using splitting dimension $$(d+1) \bmod k$$.
To satisfy steps 1 and 2 of the $$k$$-d tree construction algorithm, we recommend finding the median of the vector of points using quickselect. The quickselect algorithm allows you to find the median of the vector while achieving the constraints mentioned in step 2. We recommend that you first understand the algorithm and then write your own code from scratch to implement it. This will make debugging far, far easier.
Note that you are not allowed to use any standard library functions to sort
the data or find the median of the vector. This includes functions in
<algorithm> like std::sort and std::nth_element. For a complete list see
the functions in mp5_provided/no_sort.h.
Here’s an example of how the algorithm works on the array below.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| (3, 2) | (5, 8) | (6, 1) | (4, 4) | (9, 0) | (1, 1) | (2, 2) | (8, 7) |
With respect to splitting dimension $$0$$, we would now find the median of these points, and place it in index $$\left\lfloor\frac{0+7}{2}\right\rfloor = 3$$. (This is step 1 and 2 of the algorithm.) We could achieve this using quickselect. This yields the following array.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| (4, 4) |
What’s important to note is that the two sublists contained in indices 0–2 and 4–7, $$L_1$$ and $$L_2$$ respectively, achieve the constraint mentioned in step 2 of the $$k$$-d tree construction algorithm. (See above.) Hence, the full list may appear like this:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| (1, 1) | (3, 2) | (2, 2) | (4, 4) | (6, 1) | (5, 8) | (9, 0) | (8, 7) |
When we recursively call the algorithm on $$L_1$$ and $$L_2$$ using splitting dimension $$1$$ (step 3), we achieve the following ordering. (Follow along this example using pen and paper.)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| (1, 1) | (2, 2) | (3, 2) | (4, 4) | (9, 0) | (6, 1) | (5, 8) | (8, 7) |
This, likewise, represents the following $$k$$-d tree:
The orange colors represent nodes that were split across the 0th dimension, while the blue colors represent nodes that were split across the 1st dimension. (Why is $$(2, 2) < (3, 2)$$ with respect to the 1st dimension?)
Implementing findNearestNeighbor
Please see the Doxygen for findNearestNeighbor.
This function takes a reference to a template parameter Point and returns the
Point closest to it in the tree. We are defining closest here to be the
minimum Euclidean distance between elements. Again, if there are ties (this
time in distance), they must be decided using the Point class’s
operator<.
The findNearestNeighbor search is done in two steps: a search to find the
smallest hyperrectangle that contains the target element, and then a back
traversal to see if any other hyperrectangle could contain a closer point,
which may be a point with smaller distance or a point with equal distance, but
a “smaller” point (as defined by operator< in the Point class).
In the first step, you must recursively traverse down the tree, at each level choosing the subtree which represents the region containing the search element. (Remember that the criteria for which you choose to recurse left or recurse right depends on the splitting dimension of the current level.) When you reach the lowest bounding hyperrectangle, then the corresponding node is effectively the “current best” neighbor. Note that this search is similar to a binary search algorithm, except with the possibility of a tie across a level’s splitting dimension.
At then end of first step of the search, we start traversing back up the $$k$$-d tree to the parent node. We now want to find better matches that exist outside of the containing hyperrectangle. The current best distance defines a radius which contains the nearest neighbor. During the back-traversal (i.e., stepping out of the recursive calls), you must first check if the distance to the parent node is less than the current radius. If so, then that distance now defines the radius, and we replace the “current best” match.
Next, it is necessary to check to see if the current splitting plane’s distance from search node is within the current radius. If so, then the opposite subtree could contain a closer node, and must also be searched recursively.
During the back-traversal, it is important to only check the subtrees that are within the current radius, or else the efficiency of the $$k$$-d tree is lost. If the distance from the search node to the splitting plane is greater than the current radius, then there cannot possibly be a better nearest neighbor in the subtree, so the subtree can be skipped entirely.
Here is a reference we found quite useful in writing our $$k$$-d tree: Andrew Moore’s Kd-tree Tutorial.
You can assume that findNearestNeighbor will only be called on a valid
$$k$$-d tree.
Here is an example:
Suppose we have the same $$k$$-d tree as in Figure 1 and that the target point (in red) is $$(6,3)$$, as shown in the figure below. We wish to find the point in the $$k$$-d that is closest to the target; i.e., to determine which of the black points is closest to the red point.
To start the search, we begin a depth-first search to find the leaf node within the same splitting plane as the target node. At the root of the tree, the node is defined by the point $$(7,2)$$, with the splitting plane based on the first coordinate. Since $$6 < 7$$ (using the target coordinate’s first dimension) we search the left subtree (the grey region in the figure below).
The child node is defined by $$(5,4)$$, and the splitting plane is based on the second coordinate. Again, the target node $$(6,3)$$ is in the left subtree, so we split left.
At the next step, we hit a leaf node, $$(2,3)$$. At this point, $$(2,3)$$ becomes our current best node, and the distance from the target node to $$(2,3)$$ defines a “current best” radius, as indicated by the circle below. That is, any point outside of this radius cannot be the closest point to the target, since $$(2,3)$$ will always be closer; however, there may be a point within the radius that is closer. We now start the back-traversal to check for other nodes within this radius.
Back at the parent node, $$(5,4)$$, we see that it is closer to our target point than the current best of $$(2,3)$$. So, $$(5,4)$$ is stored as the current best, and we update the radius.
The distance from the target point to the splitting plane for the node $$(5,4)$$ is within the current radius, so we must search the other subtree, indicated by the grey region below. This can be visualized as the hypersphere (in 2-d, a circle) intersecting the region opposite the splitting plane, as shown by the red region in the figure below. We descend into the subtree and find a leaf node $$(4,7)$$, which is farther away than our current best.
We return all the way to the root node, defined by $$(7,2)$$. The distance
between this node and the target is exactly equal to the current radius. In
this case, we check Point<2>::operator<, which says our current best of $$(5,
4)$$ is less than $$(7, 2)$$, so we don’t replace the current best node.
Once again, the distance between the splitting plane defined by $$(7,2)$$ and the target point is within the current radius (i.e., the red region exists), so we must search the other subtree.
The target point is less than the splitting plane defined by the node at $$(9,6)$$, so we first descend into the left subtree.
We encounter a leaf node, $$(8,1)$$, but the distance is greater than the current best, so we don’t do anything.
We finally step back up the tree, and find there are no more regions that intersect the hypersphere (i.e., no other rectangles intersect the circle). Therefore, $$(5,4)$$ is the nearest neighbor, and our search is complete.
Function printTree
We’ve provided this function for you! It allows easy printing of the tree, with code like this:
KDTree<3> tree(v);
tree.printTree(cout);Note that the tree is printed as such:
(51,
______ 35)_____
______/ \______
(44, {84,
__ 43)_ __ 44}_
__/ \__ __/ \__
{28, (43, {60, {88,
10} 65) 30} 72}
/ \ / \ / \ / \
{14, {48, (42, (44, {59, {74, {54, {95,
15} 0} 63) 79) 0} 0} 62} 50}
\ \ \ \ \
{34, (49, {82, {75, {96,
15} 83) 20} 68} 56}
The bold dimensions are the pivot dimensions at each node. The green indicate
that the tree matched the solution tree. The { } curly braces indicate that a
node is a land mine - a point that should not be traversed in the given nearest
neighbor search, and will “explode” if you look at it. As these functions are
implemented in kdtree_extras.cpp, which will not be used for grading, please
do not modify them. All of your $$k$$-d tree code should be in kdtree.h and
kdtree.cpp.
Implementation Notes
This is a template class with one integer template parameter (i.e.
int Dim). You might be curious why we don’t just let the client specify the dimension of the tree via the constructor. Since we specify the dimension through a template, the compiler will assure that the dimension of thePointclass matches the dimension of our $$k$$-d tree.You should follow the rules of
constcorrectness and design the class to encapsulate the implementation. That is, any helper functions or instance variables should be made private.
Testing
We have provided a small number of tests for the KDTree class. The test cases
are defined in testkdtree.cpp. Be aware that these are deliberately
insufficient. You should add additional test cases to more thoroughly test your
code. You can compile the unit tests with the following command:
make testThis will create an executable named test which
you can execute with the following command to run tests for Part 1:
./test [part=1]KDTree is a templated class. Recall that template functions are not compiled
if they are never called. Make sure all of your code compiles or we will not be
able to grade your work.
Extra Credit Submission
For extra credit, you can submit the code you have implemented and tested for part one of MP 5. You must submit your work before the extra credit deadline as listed at the top of this page. See Handing in Your Code for instructions.
MP 5.2
For the second part of MP 5, you will implement the mapTiles() function which
maps TileImages to a MosaicCanvas based on which TileImage has an average
color that is closest to the average color of that region in the original
image.
HSLAPixel to Point<3> conversion.
Your points should be in H-S-L order and hue must be normalized to [0, 1]. That is, hue/360 should be the $$x$$ (0th dimension), saturation should be the $$y$$ (1st dimension), and luminance should be the $$z$$ (2nd dimension).
Classes Involved in mp5.2
In implementing mapTiles, you will need to interact with a number of classes,
including the KDTree class which you’ve built.
The source code for all these classes is provided for you, meaning you can look at their implementation if you have questions about return types, parameters, or the way the functions work.
The mapTiles() function
Please see the Doxygen for mapTiles.
mapTiles() is a function that takes a SourceImage and a vector of
TileImages and returns a MosaicCanvas pointer. It maps the rectangular
regions of the SourceImage to TileImages.
Its parameters are a
SourceImageand a constant reference to astd::vectorofTileImageobjects in that order.It creates a new dynamically allocated
MosaicCanvas, with the same number of rows and columns as theSourceImage, and returns a pointer to this object.For every region in the
SourceImage,mapTiles()should take theTileImagewith average color closest to the average color of that region and place thatTileImageinto theMosaicCanvasin the same tile position as theSourceImage’s region.map_tiles- The locations of the tiles in the mosaic are defined by aMosaicCanvas. This function should create a newMosaicCanvaswhich is appropriately sized based on the rows and columns of tiles in theSourceImage. Then, each tile in theMosaicCanvasshould be set to an appropriateTileImage, using aKDTreeto find the Nearest Neighbor for each region. Note that most of the real work here is done by building a $$k$$-d tree and using its nearest neighbor search function. Return a pointer to the createdMosaicCanvas. You can assume that the caller of the function will free it after it has been used.
You may return NULL in the case of any errors, but we will not test your
function on bad input (e.g., a SourceImage with 0 rows/columns, an empty
vector of TileImages, etc.).
Implementation Notes
- There are two classes representing a color in this portion of the MP:
HSLAPixelandPoint<3>. You will need to convert between these different representations.- Note that your points should be in H-S-L order and hue must be normalized to [0, 1]. That is, hue/360 should be the $$x$$ (0th dimension), saturation should be the $$y$$ (1st dimension), and luminance should be the $$z$$ (2nd dimension).
- Use your
KDTreeclass to find the nearest neighbor, which is the tile image that minimizes average color distances. - You can easily convert from a
TileImageto its average color usingTileImage::getAverageColor(). You will also need to convert from an average color to theTileImagethat would generate that color. You may want to use thestd::mapclass to do this.
Compiling and Running A PhotoMosaic
After finishing both the KDTree class and the mapTiles function, you can
compile the executable by linking your code with the provided code with the
following command:
makeThe executable created is called mp5. You can run it as follows:
./mp5 background_image.png [tile_directory/] [number of tiles] [pixels per tile] [output_image.png]Parameters in [square brackets] are optional. Below are the defaults:
| Parameter | Default | Notes |
|---|---|---|
background_image.png |
||
tile_directory/ |
EWS-specific | See below (default only valid on EWS) |
number of tiles |
100 | The number of tiles to be placed along the shorter dimension of the source image |
pixels per tile |
50 | The width/height of a TileImage in the result mosaic. Don’t make this larger than 75 for the provided set of TileImages |
output_image.png |
mosaic.png | .png, .jpg, .gif, and .tiff files also supported |
Additional Resources
In addition to the given code from subversion, we have provided a directory of
small thumbnail images which can be used as the tile_directory of the
photomosaic program. If you are working on EWS, then you can use
/class/cs225/mp5_pngs/ as the tile_directory. If you are working on your
own machine (including the VM), you can download them from here:
mp5_pngs.tar.bz2. If you prefer, you can download them directly to your
mp5 directory by running
wget https://courses.engr.illinois.edu/cs225/sp2018/mps/5/mp5_pngs.tar.bz2Once downloaded, you need to extract it. Do so by running
tar xjvf mp5_pngs.tar.bz2You may also use your own directory of images to create your own PhotoMosaics. However, for the supplied tests, you should use our provided images.
Testing
We have provided a simple test case for mapTiles(), which can be run with:
make test
./test [part=2]We have also provided you with a sample input sourceimage and output
mosaiccanvas, which can be tested as follows:
make
./mp5 tests/source.png /class/cs225/mp5_pngs/ 75 25 mosaic.png
wget https://courses.engr.illinois.edu/cs225/sp2018/mps/5/mosaic_soln2.png
diff mosaic.png mosaic_soln2.pngMake sure to change the second argument (/class/cs225/mp5_pngs/) to the directory
you downloaded above.
Be aware that these are deliberately insufficient. You should add additional test cases to more thoroughly test your code.
Part 3 (Creative): Your Flood Fill!
This creative part of the MP must be completed individually and must be significantly different from your partner’s creative work.
You have two weeks making an mosaic – you should show off your work! You’ll have to gather some pictures, convert them to PNGs, and generate a mosaic using your mp5 executable.
After generating your mosaic, make sure to commit it to git as mymosaic.png.
Making a great mosaic: Gathering Pictures
A good mosaic requires a lot of tile images. A baseline for a decent mosaic is ~100 tile images if the images are all different (eg: not all daylight pictures or selfies) and ~1000 for a great mosaic. You probably already have many images:
- If you have an Android, Google Photos usually [backs up your photos to the cloud at photos.google.com][https://photos.google.com/]. You can download them as a ZIP file.
- If you have an iPhone, Apple usually [backs up your photos in iCloud][https://www.icloud.com/]. You can download them as a ZIP file.
- Using a computer and a bit of time, you can download a bunch of your photos frome Facebook, Instagram, Twitter, etc.
Making a great mosaic: Converting to PNG
The program you built requires PNG files as input. Often photos are JPEG files and must be converted.
Once you have converted all of the image into PNG, place all of the images into a single directory inside of your mp5 folder. This folder will likely be very large – you should NOT commit it to git!
Making a great mosaic: Sharing and explaining what you’ve made
A mosaic looks like a fun Instagram “block” transformation at first glance, but becomes even more amazing when someone understands what they’re seeing – an image made entirely from other images.
If you share you image, it’s best if you describe what you’ve done! If you want to share it with your peers, post it with #cs225 so we can find it. :)
This MP is unique in that the story behind how you made it makes the mosaic even more awesome. Let poeple know you built a kd-tree to find the best image to place at every point in the image. Wade shared his mosaic in lecture on Wednesday.
Use #cs225, and we'll make sure to or the post
Handing in Your Code
Commit your changes in the usual way:
git add -u
git commit -m "<your message>"
git push origin masterGrading Information
The following files are used to grade MP 5:
maptiles.cpp(MP 5.2 only)maptiles.h(MP 5.2 only)kdtree.cppkdtree.hPARTNERS.txtmymosaic.png
All other files will not be used for grading.