
DFS (XKCD #761)
Assignment Description
In this lab you will:
- Use a traversal to find a particular edge in a graph.
- Find the shortest path between two vertices.
- Implement Kruskal’s minimum spanning tree algorithm.
Checking Out The Code
Get the code in the usual way.
From your CS 225 git directory, run the following on EWS:
git fetch release
git merge release/lab_graphs -m "Merging initial lab_graphs files"If you’re on your own machine, you may need to run:
git fetch release
git merge --allow-unrelated-histories release/lab_graphs -m "Merging initial lab_graphs files"your dsets from mp7 is needed in lab_graphs, remember to copy both the dsets.h and dsets.cpp files:
cd lab_graphs
cp ../mp7/dsets.cpp .
cp ../mp7/dsets.h .Since you have created these two new files, when submitting your work you will need to first:
git add dsets.h dsets.cppThis lab has a graph library already implemented for you; it is your job to
write some functions that make use of it. These functions are contained in the
namespace GraphTools, and you can implement them by editing graph_tools.h
and graph_tools.cpp. These are the only files that will be used for grading
this lab. demo.cpp shows you how that graph class can be used, and
tests.cpp calls your functions and creates output images. Some code to create
some specific graphs is located in premade_graphs.cpp. The functions there
will create graphs that represent maps of the United States, Europe, and Japan.
You can have tests.cpp call your functions on these map graphs, or on random
graphs.
The source code in this lab is documented heavily. Use this to your advantage. Above each function (including the ones you need to write), is a comment describing what the function does, its inputs, and its outputs. Hints and notes are included in the documentation above the functions you will write.
For a list of files and their descriptions, see the Doxygen for this lab.
The Graph Library
demo.cpp shows several ways that the Graph class and its functions can be
used. Use this opportunity to familiarize yourself with the available
functions. All functions are very similar (if not identical) to those described
in lecture. By default, running
make graphdemo
./graphdemowill print two graphs to your terminal and put additional graph image files in
the images/ directory.
To help you debug your code, each edge is colored according to its edge label
when graphs are printed as PNGs. Edge labels can be set with the
setEdgeLabel(Vertex source, Vertex destination, string label) function.x The coloring scheme is as follows:
"UNEXPLORED" -> black (default)
"MIN" -> blue (solution)
"MST" -> blue (solution)
"MINPATH" -> blue (solution)
"CROSS" -> red
"DISCOVERY" -> green
"VISITED" -> grey
So if this line appears in your code, graph.setEdgeLabel(source, destination, "MIN"), the
edge between vertices source and destination would appear blue to denote that the edge is
the minimum weighted edge (i.e., if you were doing findMinWeight()).
Please note that the default edge label and vertex label is empty string.
If you are doing a traversal or need to rely on the labels for any reason, you
should initialize them to some value or consider empty string as
"UNEXPLORED".
Another useful function for debugging is snapshot(), a member function of the
Graph class. By default, tests.cpp print out a picture of your graph after
you’re done with it, but what if you wanted to see how your graph labels are
changing as you traverse it? For example,
// do a BFS on the graph g
// setup snapshot feature with your image title
g.initSnapshot("myBFS");
while(...)
{
// traverse the graph
g.snapshot();
// label edges, etc
// ...
}will create a PNG for each iteration of the while loop, so you can see how
the traversal progresses. Ideally, edges will change from "UNEXPLORED" to
"DISCOVERY", "CROSS", or "VISITED". You will be able to see this by
watching the edges change color while flipping through the generated files
myBFS0.png, myBFS1.png, myBFS2.png, etc in images/.
One last bit of information: if you run
make tidyall the PNG files in images/ will be deleted. This is useful because they can
accumulate fast, especially if you are liberally using snapshot().
int GraphTools::findMinWeight(Graph & graph)
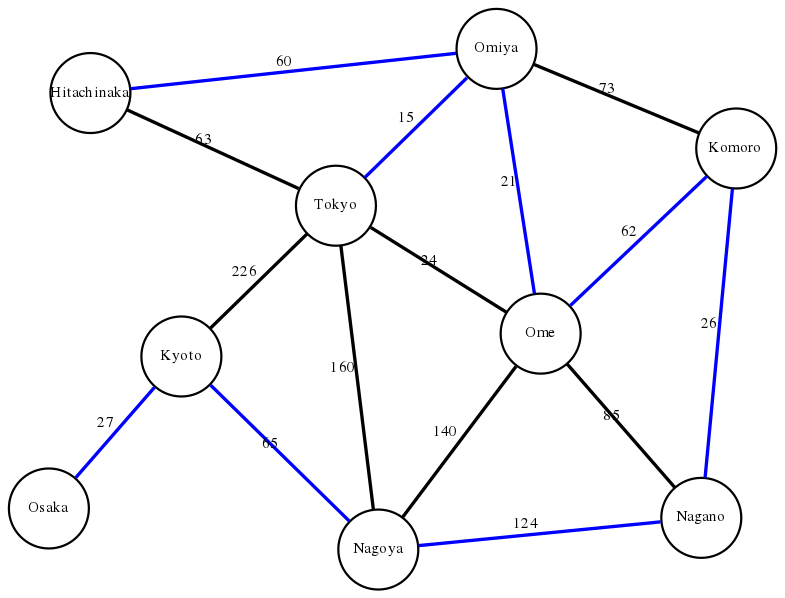
Given the map graphs of the U.S., Europe, and Japan, which two cities are closest in each one?
- U.S.: Champaign and Chicago (126 miles).
- Europe: Prague and Berlin (174 miles).
- Japan: Tokyo and Omiya (15 miles).
(Note traversal edges are also colored in this solution).
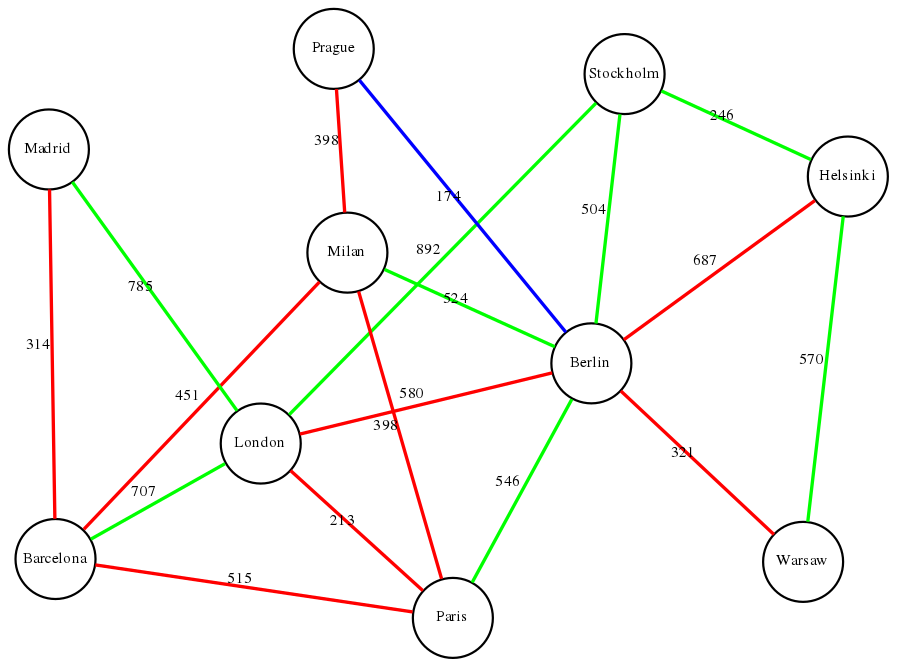
To test your code, run:
./lab_graphs weight europeto test on the Europe map (you can also use “us” or “japan”)
./lab_graphs weight randomor to test on a random graph
./lab_graphs weight random 8 47or to test on a random graph with 8 vertices and random seed 47.
int GraphTools::findShortestPath(Graph & graph, Vertex start, Vertex end)
What is the minimum number of layovers/train exchanges between two cities if the only flights/routes possible are represented by edges on the graph?
- Minimum path from KansasCity to WashingtonDC: 3 edges.
- Minimum path from London to Prague: 2 edges.
- Minimum path from Nagoya to Hitachinaka: 2 edges.
Your graph may differ (say, KansasCity->Chicago->Cincinnati->WashingtonDC),
but the minimum number of edges is the same: 3.
We will take it into consideration when grading that there may be multiple paths of minimum length.

For this task, you must return the length of the shortest path (in edges)
between two vertices. You must also color the edges in the shortest path blue
by labeling them "MINPATH".
To test your code, run
./lab_graphs path europeto test on the Europe map (you can also use “us” or “japan”) or
./lab_graphs path randomto test on a random graph or
./lab_graphs path random 8 47to test on a random graph with 8 vertices and random seed 47.
void GraphTools::findMST(Graph & graph)
What path can you create between all cities in each graph with the minimum total distance?
For this task, you must label the edges of the minimum spanning tree as "MST"
in the Graph g using Kruskal’s Algorithm.
A spanning tree connects all vertices of a graph, without creating cycles. A minimum spanning tree does the same thing, but the edges it uses to connect the vertices are of minimal weight. In other words, a minimal spanning tree uses the lightest edges possible to connect all the vertices in a graph.
In class we learn about two algorithms that accomplish this: Prim’s Algorithm and Kruskal’s Algorithm. For this lab, we will use Kruskal’s algorithm, because we already have the tools necessary to implement it. Incredibly, we can find and label the minimum spanning tree in less than 40 lines of code! Let’s take a look at the algorithm:
- Get a list of all edges in the graph and sort them by increasing weight.
- Create a disjoint sets structure where each vertex is represented by a set.
- Since a Vertex is a string but you need integers to implement disjoint set, how will you solve it?
- Traverse the list from the start (i.e., from lightest weight to heaviest).
- Inspect the current edge. If that edge connects two vertices from different sets, union their respective sets and mark the edge as part of the MST. Otherwise there would be a cycle, so do nothing.
- Repeat this until \(n-1\) edges have been added, where \(n\) is the number of vertices in the graph.
To test your code, run:
./lab_graphs kruskal europeto test on the Europe map (you can also use “us” or “japan”) or
./lab_graphs kruskal randomto test on a random graph or
./lab_graphs kruskal random 8 47to test on a random graph with 8 vertices and random seed 47.
Submitting Your Work
The following files (and ONLY these files!!) are used for grading this lab:
graph_tools.hgraph_tools.cppdsets.hdsets.cpp
All other files including any testing files you have added will not be used for grading.