ECE 486 Control Systems
Lecture 21
Pole Placement
Last time, we discussed the phenomenon of pole-zero cancellation. Further we introduced coordinate transformation or linear transformation and used a quick example to show how to convert the state-space model of a completely controllable system to Controllable Canonical Form.
In this lecture, we will learn how to assign arbitrary closed loop poles of a completely controllable system \(\dot{x} = Ax + Bu\) by means of (full) state feedback \(u=-Kx\).
Pole Placement by State Feedback
Recall a system state-space model shown in Figure 1
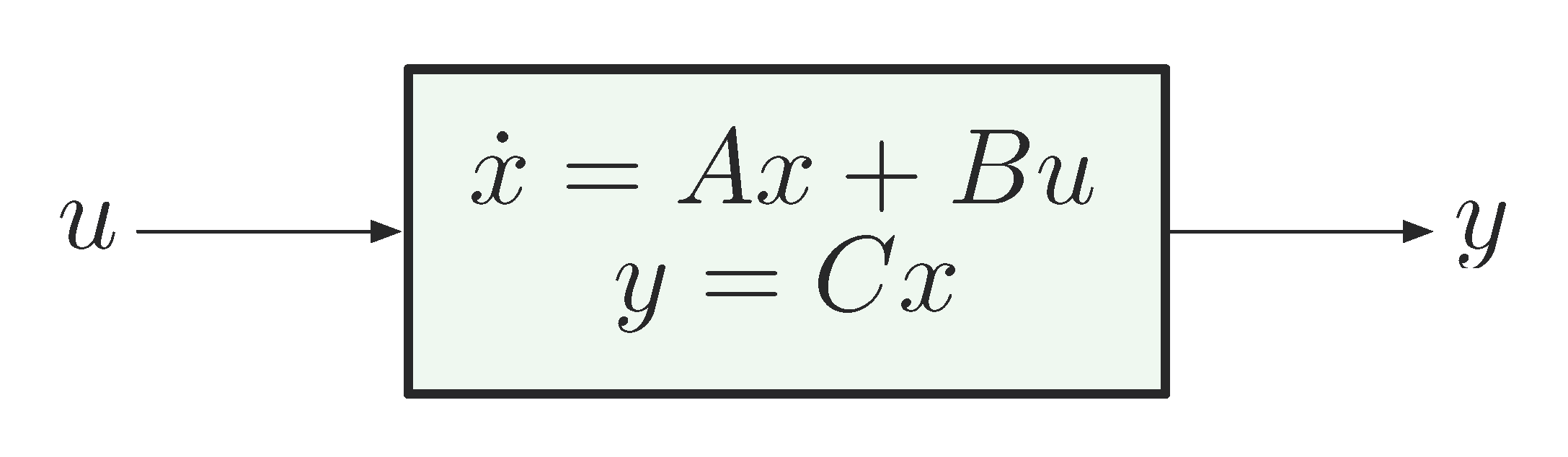
Figure 1: State-space model of a system with input \(u\) and output \(y\)
corresponds to a transfer function \(G(s)\)
\[ G(s) = C(sI-A)^{-1}B. \]
Its open loop poles are the eigenvalues of \(A\) matrix
\[ \det(sI-A) = 0. \]
We can add a controller to move the poles to desired locations, called pole placement
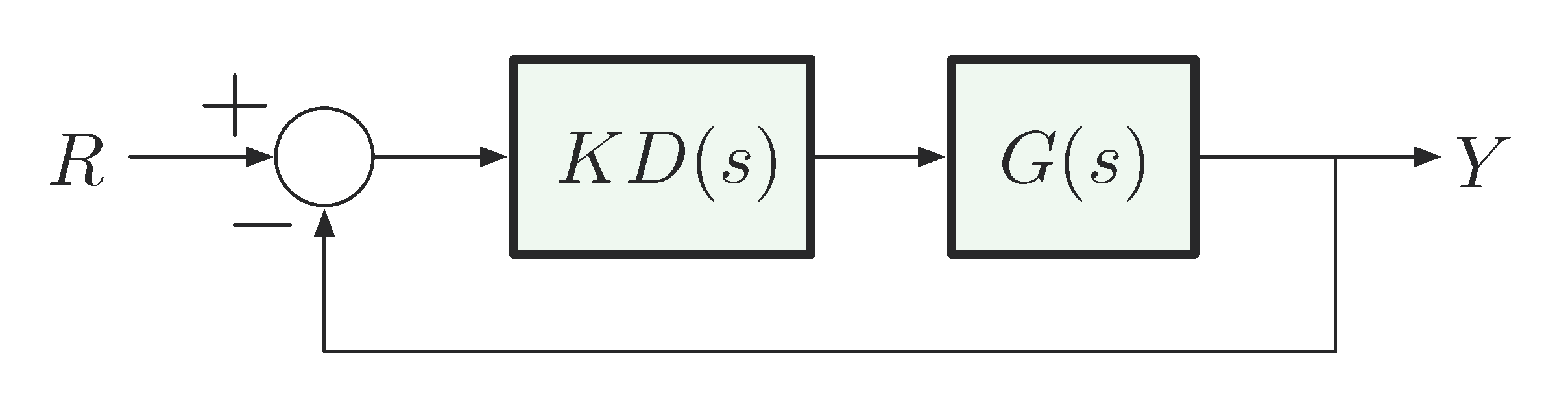
Figure 2: Pole placement via controller \(KD(s)\)
Consider the single-input system in Figure 1 with \(y = 1 x\).
\begin{align*} \dot{x} &= Ax + Bu, \, x \in \RR^n \text{ and }\, u \in \RR, \\ y &=x. \end{align*}Let’s introduce a state feedback law
\begin{align*} u &= -Ky \\ &= -Kx \\ &= -\left( \begin{matrix} k_1 & k_2 & \cdots & k_n \end{matrix}\right) \left( \begin{matrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{matrix}\right) \\ &= - (k_1 x_1 + \cdots + k_n x_n). \end{align*}Then the closed loop system becomes
\begin{align*} \dot{x} &= Ax - BKx \\ &= (A-BK)x \\ y &= x. \end{align*}If we enclose the open loop system with feedback \(K\) and reference \(r\), as shown in Figure 3, we can derive the closed loop transfer function \(\frac{Y}{R}(s)\) as follows.
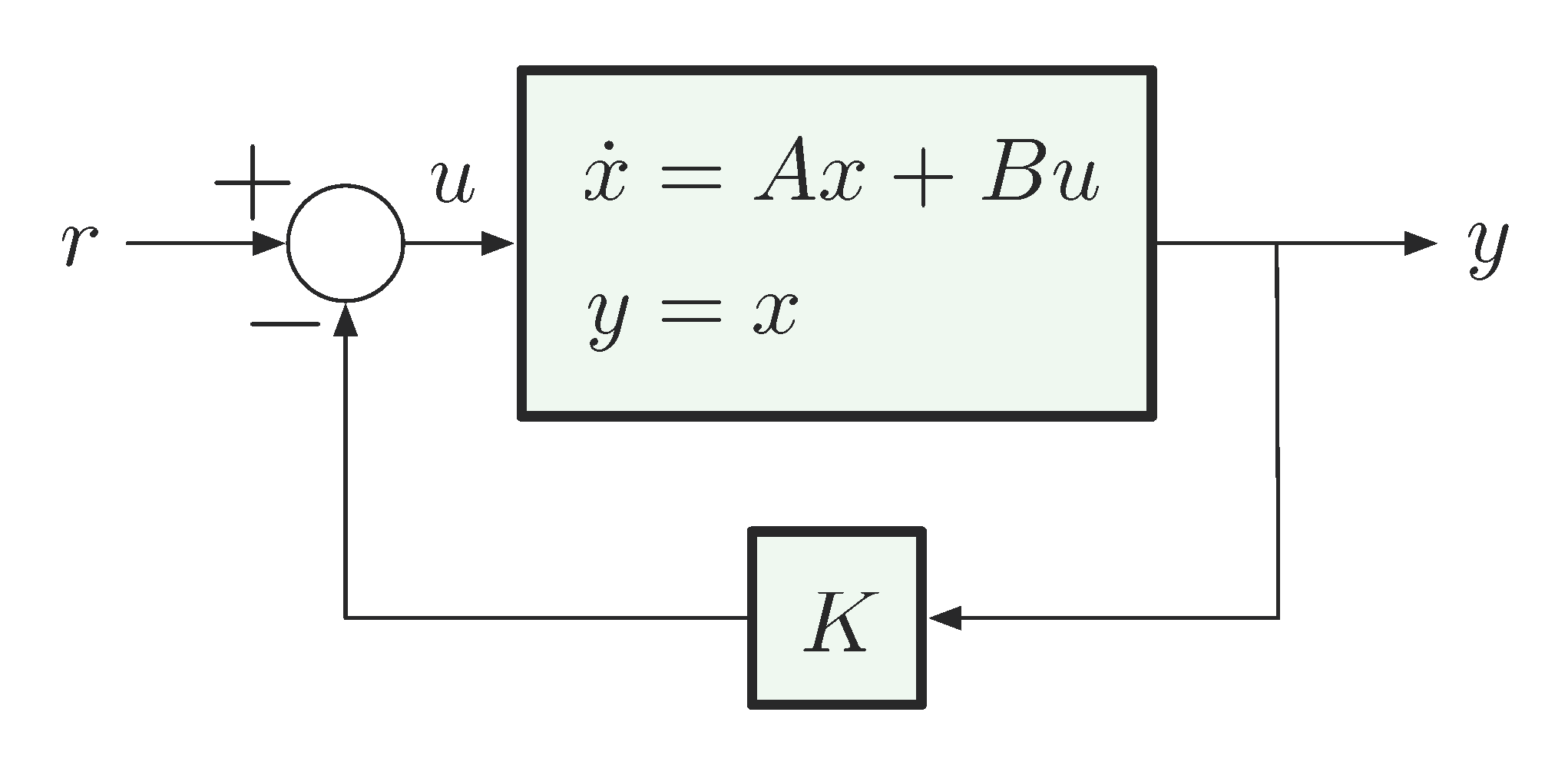
Figure 3: State feedback \(K\) encloses system \((A, B, I, 0)\) with reference \(r\)
Take the Laplace transform, we have
\begin{align*} sX(s) &= (A-BK)X(s) + BR(s), \\ Y(s) &= X(s). \\ \implies Y(s) &= \underbrace{(sI-A+BK)^{-1}B}_{G}R(s). \end{align*}We notice the closed loop poles are just the eigenvalues of \(A-BK\).
Pole Placement: Assigning closed-loop poles \(=\) Assigning eigenvalues of \(A-BK\).
Now we will see that this is particularly straightforward if the system model \((A,B,C,D)\) is in CCF, i.e., with
\begin{align*} A &= \left( \begin{matrix} 0 & 1 & 0 & \ldots & 0 & 0 \\ 0 & 0 & 1 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \ldots & 0 & 1 \\ -a_n & -a_{n-1} & -a_{n-2} & \ldots & -{a_2} & -{a_1} \end{matrix} \right), \, B = \left( \begin{matrix} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end{matrix}\right). \end{align*}Claim: Let
\begin{align*} A &= \left( \begin{matrix} 0 & 1 & 0 & \ldots & 0 & 0 \\ 0 & 0 & 1 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \ldots & 0 & 1 \\ -a_n & -a_{n-1} & -a_{n-2} & \ldots & -{a_2} & -{a_1} \end{matrix} \right). \end{align*}Then
\[ \det(sI-A) = s^n + a_1 s^{n-1} + \cdots + a_{n-1} s + a_n. \]
The last row of the \(A\) matrix in CCF consists of the coefficients of the characteristic polynomial in reverse order, with “\(-\)” signs.
Proof: We prove the claim by induction. We shall induct on natural number \(n\).
The base case \(n = 2\) is obvious.
Assuming true for \(n = k \geq 2\), consider a \((k+1)\times (k+1)\) matrix \(A_{k+1}\) of the form in the claim.
Its determinant can be written as
\begin{align*} \det (sI - A_{k+1}) &= (-1)^{1+1}\cdot s \cdot \det (sI - A_k) + (-1)^{1+(k+1)}\cdot a_{k+1}\cdot (-1)^k \\ &= s (s^k + a_1 s^{k-1} + \cdots + a_{k-1} s + a_k) + a_{k+1} \\ &= s^{k+1} + a_1 s^k + \cdots + a_k s + a_{k+1}. \end{align*}The first equality uses the fact that we can calculate the determinant by expansion by minors using the two entries \(s\) and \(-a_{k+1}\) in the first column.
The second equality uses the induction hypothesis for \(n = k\).
Using this claim, we shall see that the closed loop poles can be assigned by state feedback. By Laplace transforms,
\begin{align*} \dot{x} &= Ax + Bu \\ A &= \left( \begin{matrix} 0 & 1 & 0 & \ldots & 0 & 0 \\ 0 & 0 & 1 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \ldots & 0 & 1 \\ -a_n & -a_{n-1} & -a_{n-2} & \ldots & -{a_2} & -{a_1} \end{matrix} \right), \, B = \left( \begin{matrix} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end{matrix}\right) \end{align*}Represent this as a system of ODEs
\begin{align*} \begin{array}{l} &\dot{x}_1 = x_2 & X_2 = sX_1 \\ &\dot{x}_2 = x_3 & X_3 = sX_2 = s^2X_1\\ &\hspace{8mm}\vdots & \hspace{9mm}\vdots \\ &\dot{x}_{n-1} = x_n & X_n = s X_{n-1} = \ldots = s^{n-1}X_1 \\ &\dot{x}_n = -\sum^n_{i=1} a_{n-i+1}x_i + u, & sX_n = -(a_n + a_{n-1}s + \cdots + a_1 s^{n-1})X_1 + U. \end{array} \end{align*}The last line gives us
\[ \underbrace{\left(s^n + a_1 s^{n-1} + \cdots + a_n\right)}_{\text{characteristic polynomial}}X_1 = U. \]
Recall
\begin{align*} A &= \left( \begin{matrix} 0 & 1 & 0 & \ldots & 0 & 0 \\ 0 & 0 & 1 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \ldots & 0 & 1 \\ -a_n & -a_{n-1} & -a_{n-2} & \ldots & -{a_2} & -{a_1} \end{matrix} \right) \\ BK &= \left( \begin{matrix} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end{matrix}\right) \left(\begin{matrix} k_1 & k_2 & \ldots & k_n \end{matrix}\right) \\ &= \left( \begin{matrix} 0 & 0 & 0 & \ldots & 0 & 0 \\ 0 & 0 & 0 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \ldots & 0 & 0 \\ k_1 & k_2 & k_3 & \ldots & k_{n-1} & k_n \end{matrix} \right) \\ \implies A-BK &= \left( \begin{matrix} 0 & 1 & 0 & \ldots & 0 & 0 \\ 0 & 0 & 1 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \ldots & 0 & 1 \\ -(a_n+k_1) & -(a_{n-1}+k_2) & -(a_{n-2}+k_3) & \ldots & -({a_2}+k_{n-1}) & -(a_1+k_n) \end{matrix} \right) \end{align*}Therefore \(A - BK\) is also in some state-space model in CCF. Indeed, it is the “\(A\)” matrix of the state-space model of closed loop system in Equation \eqref{d21_eq1}. \(\det \big(sI - (A-BK) \big)= 0\) determines the eigenvalues of \(A - BK\), i.e., the closed loop poles. By the claim we proved above,
\begin{align*} &\det\big(sI-(A-BK)\big) = s^n + (a_1+k_{n})s^{n-1} + \ldots + (a_{n-1}+k_2)s + (a_n+k_1). \end{align*}Observation: When the system is in Controllable Canonical Form (CCF), each control gain affects one and only one of the coefficients of the characteristic polynomial, and these coefficients can be assigned arbitrarily by a suitable choice of \(k_1,k_2,\ldots,k_n\).
Hence the name Controllable Canonical Form — convenient for control design.
We can summarize the general procedure for any completely controllable system.
- Convert state-space model of the system to CCF using a suitable invertible coordinate transformation \(T\); such a transformation exists by controllability.
- Solve the pole placement problem in CCF in the new coordinates.
- Convert the solution in CCF framework back to original coordinates.
Example: Consider the given state-space model below,
\begin{align*} \dot{x} &= Ax + Bu, \text{ with }\\ A &= \left(\begin{matrix} -15 & 8 \\ -15 & 7 \end{matrix}\right),\, B = \left(\begin{matrix} 1 \\ 1 \end{matrix}\right). \end{align*}Find a state feedback to place closed loop poles at \(-10\pm j\).
Solution: Step 1: Check the controllability and find the linear transformation to convert our state-space model to CCF. (We steal the transform \(T\) from last time.)
\begin{align*} T &= \left( \begin{matrix} 1 & -1 \\ 0 & 1 \end{matrix}\right) \\ \implies \bar{A} &= TAT^{-1} \\ &=\left( \begin{matrix} 0 & 1 \\ -15 & -8 \end{matrix}\right),\\ \bar{B} &= TB \\ &=\left( \begin{matrix} 0 \\ 1 \end{matrix}\right). \end{align*}Step 2: Find \(u = -\bar{K}\bar{x}\) to place closed-loop poles at \(-10 \pm j\).
The desired characteristic polynomial is
\begin{align*} (s+10+j)(s+10-j) &= (s+10)^2 + 1 \\ &= s^2 + 20s + 101. \end{align*}Thus the closed loop system matrix should be
\begin{align*} \bar{A} - \bar{B}\bar{K} = \left( \begin{matrix} 0 & 1 \\ -101 & -20\end{matrix}\right). \end{align*}On the other hand, we know
\begin{align*} \bar{A} - \bar{B}\bar{K} &= \left( \begin{matrix} 0 & 1 \\ -(15+\bar{k}_1) & -(8+\bar{k}_2)\end{matrix}\right). \end{align*}Matching the matrix entries, we get \(\bar{k}_1 = 86, \, \bar{k}_2 = 12\).
This gives the control law
\begin{align*} u = -\bar{K}\bar{x} = -\left(\begin{matrix} 86 & 12 \end{matrix}\right)\left(\begin{matrix} \bar{x}_1 \\ \bar{x}_2 \end{matrix}\right). \end{align*}Step 3: Convert obtained state feedback back to the old coordinates.
\begin{align*} u &= -\bar{K}\bar{x} \\ &= -\underbrace{\bar{K}T}_{K}x. \end{align*}Therefore,
\begin{align*} K &= \bar{K}T \\ &=\left(\begin{matrix} 86 & 12 \end{matrix}\right)\left( \begin{matrix} 1 & -1 \\ 0 & 1 \end{matrix}\right) \\ &= \left(\begin{matrix} 86 & -74 \end{matrix}\right). \end{align*}The desired state feedback control law therefore is
\begin{align*} u = \left(\begin{matrix} -86 & 74 \end{matrix}\right) \left( \begin{matrix} x_1 \\ x_2 \end{matrix}\right). \end{align*}