Physics 113 - Fall 00
Sample Final Exam Questions
1. The molar specific heat, cV, of a block of iron at T = 1 K is
The specific heat of solids drops to zero as the temperature approaches zero. At low temperatures, the solid can be approximated by a two-level system (Lecture 11) where the specific heat goes to zero as the temperature goes to zero.
2. An ideal Carnot engine acting as a refrigerator has one isothermal process in which Qfood joules of heat from the food is extracted in order to compress the working fluid of the refrigerator. The change of entropy of the working fluid, DSfluid, is related to the change in entropy of the food, DSfood, by
Heat is extracted from the food so its entropy decreases by Qfood/TC, i.e.
D
Sfood= -Qfood/TCThat heat is added to the working fluid of the refrigerator so the entropy of the working fluid increases by the same amount
D
Sfluid= Qfood/TC = -DSfood
3. A thermodynamic system has entropy S given by the expression ![]() . Here U is the internal energy, V the volume, k is Boltzmann's constant and a is a (different) constant. Which expression below gives the temperature of the system?
. Here U is the internal energy, V the volume, k is Boltzmann's constant and a is a (different) constant. Which expression below gives the temperature of the system?
(a) T = kaV/Ö U
(b)
T = Ö U/ kaV(c) T = kaVÖ U
The definition of temperature is
1/T = dS/dU)V=const
dS/dU)V=const = kaV/
Ö UT =
Ö U/kaV4. Suppose an rubber band starts with a length of 10 cm and a temperature of 273oK. Its state is changed in one of two ways:
i) The band is heated to a temperature of 290 K. Then, being kept at this new temperature, it is slowly stretched until its length is 15 cm. In this entire process its entropy changes by an amount
DS1ii) The band is slowly stretched to a length of 15 cm while being kept at a temperature of 273 K. Then, while remaining at this length, it is slowly heated to 290 K. In this entire process its entropy changes by an amount
DS2.(a) DS1 < DS2
(b)
DS1 = DS2(c) DS1 > DS2
In both cases the rubber band starts in state one (T = 273, L = 10 cm) and ends up in state two (T = 290 K, L = 15 cm). Since S is a state function the change in S in the two processes has to be the same!
The next four questions pertain to the following figure:
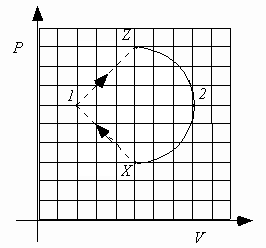
A heat engine consists of 0.10 moles of an ideal monatomic gas that is confined to a cylinder with a piston. The gas is taken from state X to state 1, to state Z, to state 2 and then back to state X. The PV diagram below shows the values of pressure and volume of the gas.
5. What is
DU1, the change in internal energy in the process X® 1® Z?i.e.
DU1 = U(Z) - U(X).
a) DU1 < 0
b) DU1 = 0
c
) DU1 > 0Because the internal energy is a state function, the only relevant information is that the system starts in state X and ends in the state Z. Because VZ = VX and
pZ > pX, TZ > TX (ideal gas law), UZ > UX (U
6. What is W1, the work done by the gas in the process X
a) W1 < 0
b) W1 = 0
c
) W1 > 0The work done from X
® 1 is negative, but the work done from 1 ® Z is positive and of a larger magnitude (the area under the curve 1 ® Z is larger than the area under the curve X ® 1). Therefore the net work done is W1 = WX ® 1 + WZ ® 1 > 0.
7. Compare |W2|, the absolute value of the work done by the gas during process Z
® 2® X to |W1|, the absolute value of the work done by the gas during process X® 1® Z.
a) |W2| < |W1|
b) |W2| = |W1|
c
) |W2| > |W1|The absolute value of the work done by the gas during the process Z
® 2® X is equal to the area of the semicircle bounded by Z, 2 and X. The absolute value of the work done by the gas during the process X® 1® Z is equal to the area of the triangle bounded by X, 1 and Z. Since the area of the semicircle is larger than the area of the triangle (the triangle will fit inside the semicircle), |W2| > |W1|.
8. Now consider a different situation. Compare Q2, the heat added to the gas during the reverse process X
® 2® Z, with Q1, the heat added to the gas during the original process X® 1® Z. (Consider the sign of the heat in your ranking such that all positive values are greater than all negative values, i.e., +4 > -8).
a)
Q2 < Q1b) Q2 = Q1
c) Q2 > Q1
Now, comparing the two processes starting at X and ending at Z, the first going through point 1 and the second going through point 2
D
U1 = DU2since U is a state function. Writing them out
D
U1 = Q1 - W1 = DU2 = Q2 - W2This time W2 < 0 (W1 is unchanged, W1 > 0) so we can write
Q1 - W1 = Q2 + |W2|
Q1 - W1 - |W2| = Q2
Finally, since W1 and |W2| are both > 0, Q2 must be less than Q1
The next two questions pertain to the following situation:
In the atmosphere of a certain planet, the pressure at an altitude of 1 km is 1/2 that at the surface. The gravitational acceleration on the planet is 30 m/s2, the atmosphere is made up entirely of nitrogen gas (mN
2 = 4.64x10-26 kg) and is at a uniform temperature, T.9. What is the temperature of the atmosphere T?
a) T = 48.5 K
b) T = 100.7 K
c
) T = 146 Kd) T = 193 K
e) T = 226 K
The ratio of the pressure at height h to that at the surface is
p(h)/p(0) = e-mgh/kT
Therefore the temperature T can be determined from the pressure ratio
-mgh/kT = ln[p(h)/p(0)]
T = -mgh/{k ln[p(h)/p(0)]}
= -4.64x10-26 30 1000/1.38x10-23/ln(1/2)
= 146 K
10. Relative to the pressure, p(0), at the surface, what is the pressure, p(5) an altitude of 5 km?
The ratio of pressures is
p(5)/p(0) = e-mg5/kT = (e-mg1/kT)5
but we know e-mg1/kT = 1/2 from the statement of the problem, hence p(5)/p(0) = (1/2)5
11. The temperature of a summer day is 37 oC and the inside of your house is a comfortable 21 oC . A certain window in your house, 1 m x 0.5 m has a thickness of 5 cm. If the rate of heat flow into the house is 400 W, what is the thermal conductivity of the window,
k?(a)
k = 0.05 W/m·K(b)
k = 0.125 W/m·K(c)
k = 0.75 W/m·K(d)
k = 1.25 W/m·K(e)
k = 2.5 W/m·KFrom lab 2, we know that the thermal conductivity,
k, is related to the heat flow, q, byq =
k A DT/Lwhere A is the area of the surface, DT is the temperature difference and L is the thickness of the surface. Therefore
k
= qL/A DT= 400 W 0.05m/0.5 m2/16 K
= 2.5 W/m·K
12. Lead melts at 327 oC (at 1 atm pressure) and the latent heat of melting is 25 kJ/kg. At a temperature of 326 oC, what is the relation between the free energies, F, of solid and liquid lead?
(a) Gsolid > Gliquid
(b) Gsolid = Gliquid
(c) Gsolid < Gliquid
At a temperature like 326
oC, below the solid-liquid equilibrium temperature of 327 oC, the solid phase is what we expect therefore its free energy has to be the lowest.
13.
A sample of SF6 (sulfur hexafluoride) gas, initially with volume Vi = 0.1 m3 and temperature Ti = 250 K, expands adiabatically to Vf = 0.3 m3. What is Tf, the final temperature of the SF6? Assume that SF6 is an ideal gas.(a) Tf = 125 K
(b) Tf = 173 K
(c) Tf = 258 K
(d) Tf = 367 K
(e) Tf = 426 K
SF6 is a polyatomic gas so
a = 3. The adiabatic relationship pVg = const can be manipulated to the form VTa = const using the ideal gas lawpV
g = nRTV g/V µ TV g-1 = TV1/aor VT
a = const. Therefore the final temperature isTf = (Vi/Vf)1/3Ti = (1/3)1/3 250 K
14. What is
DS, the change in the entropy of ten moles of an ideal monatomic gas that is expanded slowly and isothermally at a temperature of 293K from a pressure of 2 atm to a pressure of 1 atm?(a) DS = 21.7 J/K
(b)
DS = 57.6 J/K(c)
DS = 203.4 J/K(d) DS = 212.6 J/K
(e) DS = 841 J/K
First what is dQ for such a process? Since dU = 0 for an isothermal process dQ = -dW = pdV = nRTdV/V. The entropy dS = dQ/T for this slow process so the total change in entropy
DS isD
S = nR ò dV/V = nR ln(Vf/Vi)Now Vf/Vi = pi/pf for an ideal gas at constant temperature so finally
D
S = nR ln(pi/pf) = 10 8.31 ln(2)
The next two questions pertain to the following situation:
Ten atoms are placed in a magnetic field. We will consider the effect of the magnetic field on the magnetic moments of the atoms. The magnitude of the "energy" difference between spin "up" atoms and spin "down" atoms is
DM = 1.01 x 10-26 J/Tesla, and the magnetic field is pointing "up".15. If the magnetic field is 1 Tesla and the temperature is 300 K, what is the ratio of probabilities, RP, for a single atom to have its spin "up" relative "down"?
For this two-level system (two energies differing by
DM·B) we use the Boltzmann factorPup = const·e+
DMB/kT, Pdown = const·e-0/kTNote that it doesn't matter where we take the zero of the energy - here we take it to be the energy of the "down" state. So Pup/Pdown = e+
DMB/kT a number very close to one. The probability for hydrogen atoms (which these are) to have spin up relative to down in a typical MRI is only a few parts in a million!
16. What is the average number of spin "up" atoms, Nup, at temperature T?
The probability of spin up is calculated in question 19 - the first problem is to find the constant. We know that the sum of all probabilities must be one
Pup + Pdown = const(
e+DMB/kT +1) = 1therefore
Pup =
e+DMB/kT /(e+DMB/kT +1)and if there are 10 total particles Nup is just 10
·Pup17. It has been proposed that we use H2 as our new energy source. H2 may be obtained from water by electrolysis. Which of the following most accurately and completely describes the status of this idea?
The free energy of the product (water) is the same as that of the fuel (water). Therefore the most work that can be extracted, ideally, is zero. Real devices will be worse.
18. The latent heat of the water-steam phase transition at p=1 atm and T=100oC is 2256 kJ/kg. What is the entropy change
DS as the liquid vaporizes?The vapor is the high entropy phase (found at high T). So
DS is positive. DS=QL/T. Remember, that’s absolute T.
The next 2 questions pertain to the following situation
A tray holds 4 coins, all initially with "tails" facing upward.
19. The tray is continuously ‘jostled’, so that the 4 coins jump and flip randomly on the tray, causing all available ‘microstate’s of this system to become possible. What is the entropy of the 4 coin system in this "jostled" state?
a.
s = 0b.
s = 1.4c.
s = 1.8d.
s = 2.1e.
s = 2.8
There are 16 possible states, so
s is ln(16).
20. If the "jostling" is stopped, so that the 4 coins come to rest in a specific configuration of "heads" and "tails," what is the probability P that the 4 coin system will be found in its equilibrium configuration. I.e. 2 heads and 2 tails?
a. P = 0.125
b.
P = 0.25c. P = 0.375
d. P = 0.50
e. P = 0.625
There are only 4!/(2!2!)=6 ‘microstates’ with 2H, 2T. That’s out of 16 equally likely ‘microstates’.
The next 2 questions pertain to the following situation
A balloon containing 0.25 mol of helium rises from an altitude at which the pressure is 90 kPa to an altitude at which the pressure is 67 kPa. During this ascent, the gas in the balloon maintains a constant temperature of 280 K.
21. How much work W does the gas in the balloon do during this process?
a. W = - 213 J
b.
W = - 86 Jc. W = 0 J
d. W = 65 J
Usual isothermal expansion of ideal gas, Wby= nRT ln(VF/Vi)= nRT ln(pi / pF)
22. How much heat Q does the gas absorb during this process?
a. Q = -W
b.
Q = 0c. Q = W
At fixed T for ideal gas, U is fixed. So Wby must be replaced by Qin.
23. Consider 1 mole of N2 gas at p = 1 atm in a volume of 1 liter. The gas undergoes an isothermal compression to a volume of 0.5 liters. Assuming that the N2 is an ideal gas, what is the change in entropy
DS?a.
DS = 0b.
DS = 0.0823 l-atm/Kc.
DS = -0.0570 l-atm/Kd.
DS = -0.0823 l-atm/Ke.
DS = -0.132 l-atm/K
D
S= nRln(Vf/Vi)= ln(2)*0.082 liter-atm/K