ECE 486 Final Project Report
Required font settings: Times New Roman, 11pt, with page numbers
Note: In Spring 2016, credit for each demo changes and Chapter 6 and 7 are no longer extra credit chapters; they are required.
One report will be submitted per group. The final report concentrates on the two controllers that stabilize the pendulum in the inverted configuration--primarily sections 4 and 5 of the packet. The report is worth 130 points out of 250 total points for the final project and 1000 total points for the lab.
Style Points (maximum of 0, min -50)
- This is a formal report and therefore, it should flow well. Treat it as a unit and transition from section to section. Equations, figures and tables must be labeled or captioned;
- Keep in mind that it is the quality of the report, not the length, that will determine the score. Please do not submit lengthy reports; the necessary material can be concisely stated in 5-7 pages (not including the cover page). A suggested maximum length for each section of the report is provided in the outline below;
- Please also include your SIMULINK diagrams printout in your final project report.
Put your report in the following order:
-
Cover Sheet (1 page)
- All formatting should be plain text, except for your names, which should be in boldface.
- Your names
- ECE 486: Final Project Report
- [Semester] [year]
- TA's name
- day of lab section
Introduction (1 paragraph, 10 pts)-
Describe the system (1 paragraph of text):
- sensors (and number of) 3pts
- actuators (and number of) 3pts
- the equilibrium positions (and whether these are stable or unstable configurations) 3pts
- program used for implementing the controllers 1pt
-
Derive and explain the mathematical model:
- Derivation of differential equations from Lagrangian 5pts
- Linearization into state space form 5pts
- 1. Explain (in words) the development of the PD control (two-state and three-state feedback controllers in Chapter 4) with friction compensation (system identification in Chapter 2). How did you arrive at the values of your friction compensator? Was friction compensation beneficial to your state feedback controller or not, and why? (1-2 paragraphs of text) 10pts
-
2. Provide a mathematical proof that the linearized, frictionless closed-loop system is stable in the inverted position. That is, prove that theta_p(t) goes to pi as time t goes to infinity for the 3-state feedback controller you designed. First, show that the only place where
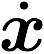 is zero is at your linearized equilibrium position. Then, show that for the linearized system
is zero is at your linearized equilibrium position. Then, show that for the linearized system
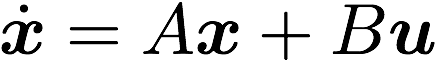 ,
,
Hint: First, substitute your control in for u. You should arrive at a differential equation with x as the only variable. Set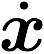 to zero and solve for x to find the equilibrium points. Now, note that we don't care what theta_r is, and that theta_r doesn't affect any of the other states. So, to check that [0 0 whatever 0] a stable equilibrium, create a smaller 3x3 A matrix and 3x1 B matrix where your states are delta_theta_p, theta_p_dot, and theta_r_dot. If this smaller system (including your 3-state feedback) is stable, then delta_theta_p, theta_p_dot, and theta_r_dot all converge to 0, and [0 0 whatever 0] is a stable equilibrium. You must use Microsoft Equation Editor, LaTeX, or a comparable program to generate equations.
to zero and solve for x to find the equilibrium points. Now, note that we don't care what theta_r is, and that theta_r doesn't affect any of the other states. So, to check that [0 0 whatever 0] a stable equilibrium, create a smaller 3x3 A matrix and 3x1 B matrix where your states are delta_theta_p, theta_p_dot, and theta_r_dot. If this smaller system (including your 3-state feedback) is stable, then delta_theta_p, theta_p_dot, and theta_r_dot all converge to 0, and [0 0 whatever 0] is a stable equilibrium. You must use Microsoft Equation Editor, LaTeX, or a comparable program to generate equations. - 3. From your Simulink simulations of the RWP, give the maximum IC deviation, pulse disturbance, and constant perturbation that the controller can stabilize. (1 table of values) 10pts
- 4. From your Windows Target implementation, describe the behavior of the system caused by your controller. (1 paragraph) 10pts
Full State Feedback Control with Decoupled Observer (2-3 pages, 50 pts)- 1. Explain the following: Why are observers used? Why can we decouple the 4-state observer design into two 2-state observers? What is the advantage of this versus a single 4-state observer? 10pts
-
2. You already proved that the 3-state feedback controller stabilizes the pendulum in the inverted configuration. Now prove that the observer states converge to the real states over time. That is, show that the error between the actual states and estimated states
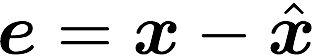
Hint: Differentiate the equation for the error. Next substitute the equations you have for x_dot, xhat_dot, and u. You should end up with a differential equation with the error e as the only variable. Next, prove that the poles are stable. Set e_dot equal to zero and show that e = [0,0,0,0] is the only stable equilibrium for this equation. - 3. From your Simulink simulations of the RWP, give the maximum IC deviation, pulse disturbance, and constant perturbation that the controller can stabilize. (1 table of values) 10pts
- 4. From your Windows Target implementation, describe the behavior of the system caused by your controller with the observer. (1 paragraph) 10pts
Conclusions (1 paragraph of text, 10 pts)- Which controller performed better? You will need to define your standard of judging performance of one controller over the other.
Extra Credit (1/2 page each, 35 possible pts)- Explain your approach to the two optional sections. What techniques did you use? Also include your Windows Target model(s) in an appendix. Note: these sections do not count against your total number of pages
Thanks for your hard work this semester, everyone! Good luck with final exams.



