Resistance in a Circuit
Find the resistance over an unknown resistor
Learn It!
Pre-Requisite Knowledge
To understand this section, you need to know the
following concepts:
- Voltage and Current Concepts
- Ohm's Law
- Resistivity
Goal
Find Resistance
Find the resistance across the unknown
resistor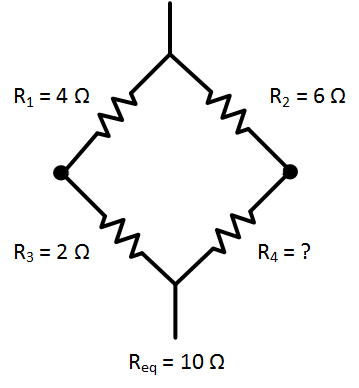
Given the resistances of three elements, what must the resistance
of the fourth element be to make the equivalent resistance equal to the desired
value?
Part 1
Stretch the Circuit
This is the first step to most equivalent resistance
problems. Redrawing and stretching out the circuit makes solving these problems
easier.

Luckily, we just need to bend the corners a little to get it
to line up.
Part 2
Solving for the last resistor
Since one of the resistances is an unknown, we can't just
reduce numerically, we have to use algebra to find the solution.
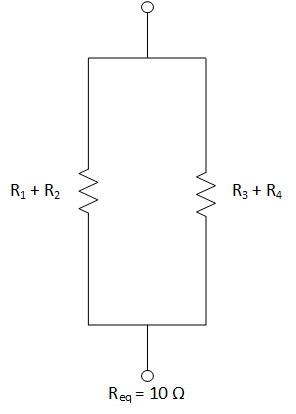
We can see two easy series resistances, \(R_1\) and
\(R_2\) are in series, and \(R_3\) is in series with the unknown \(R_4\).
We make our reductions, but we will do things symbolically. Let's use our new notation, and write it this way \(R_1+R_2\) should be read "Resistor 1 is in series with resistor two". When written symbolically in this context, the \(R's\) represent objects, not numbers.
This notation makes solving problems fast once you recognize combinations easily.
We make our reductions, but we will do things symbolically. Let's use our new notation, and write it this way \(R_1+R_2\) should be read "Resistor 1 is in series with resistor two". When written symbolically in this context, the \(R's\) represent objects, not numbers.
This notation makes solving problems fast once you recognize combinations easily.
\[(R_1 + R_2) || (R_3 + R_4)\]
These combinations are immediately recognizable as
parallel. To write this, we use the \(||\) symbol. This statement should be read
"The series combination of \(R_1\) and \(R_2\) is in parallel with the series
combination of \(R_3\) and \(R_4\)".
+
?
Order of operations for + and ||

Parentheses matter! The \(||\) parallel operator
goes before the + series operator, similar to how multiplication is done
before addition. \(||\) is not any kind of multiplication, though.
\[R_{eq} = \dfrac {1}{\dfrac{1}{R_1 + R_2} + \dfrac{1}{R_3 +
R_4}}\]
Let's turn this statement into an equation we can solve.
We've got one equation with only one unknown \(R4\), so we are in the clear.
\[R_{eq} = \dfrac{(R_1 +
R_2)(R_3+R_4)}{R_1+R_2+R_3+R_4}\]
Since we have exactly two elements in parallel, we can use
the product-over-sum rule instead. It is often easier to manipulate that way.
\[ \begin {align} 10 &=
&(4+6)*&\dfrac{2+R_4}{4+6+2+R_4} \\ 10 &=
&(10)*&\dfrac{2+R_4}{12+R_4} \end{align} \]
We can work it totally symbolically, but let's plug in our
knowns at this time. Since they can combine easily, we will have fewer symbols to manipulate.
If these were not nice, whole numbers we would not want to do this yet.
\[2+R_4 = 12+R_4\]
Cancel the \(10\)'s and multiply both sides by the
denominator
★
\[2 \neq 12 \\ \text {No Solution}\]
We arrive at the impossible answer \(2=12\). Since this is
impossible, that means our original task was impossible.
There is no possible finite resistor \(R_4\) that can make the equivalent resistance equal \(10\) in this circuit
This problem solving strategy still works on problems that have solutions.
There is no possible finite resistor \(R_4\) that can make the equivalent resistance equal \(10\) in this circuit
This problem solving strategy still works on problems that have solutions.


