Kirchhoff's Laws
Using KCL to find currents through generic elements
Learn It!
Pre-Requisite Knowledge
To understand this section, you need to know the following concepts:
Goal
Using KCL
Use KCL to find the currents through generic elements in a circuit

Find the values of \(I_1\) and \(I_2\) in the diagram at left.
\( \begin{equation} a. I_1 = 0.3\text{ A}\text{ and } I_2 = 0.6\text{ A} \\b. I_1 = 0.3\text{ A}\text{ and } I_2 = 0.4\text{ A} \\c. I_1 = 0.4\text{ A}\text{ and } I_2 = 0.4\text{ A} \\d. I_1 = 0.4\text{ A}\text{ and } I_2 = 0.5\text{ A} \\e. I_1 = 0.5\text{ A}\text{ and } I_2 = 0.6\text{ A} \end{equation} \)
\( \begin{equation} a. I_1 = 0.3\text{ A}\text{ and } I_2 = 0.6\text{ A} \\b. I_1 = 0.3\text{ A}\text{ and } I_2 = 0.4\text{ A} \\c. I_1 = 0.4\text{ A}\text{ and } I_2 = 0.4\text{ A} \\d. I_1 = 0.4\text{ A}\text{ and } I_2 = 0.5\text{ A} \\e. I_1 = 0.5\text{ A}\text{ and } I_2 = 0.6\text{ A} \end{equation} \)
Part 1
Find one unknown current
\(\Sigma I_{in}\; =\; \Sigma I_{out}\)
KCL is "Kirchhoff's Current Law." It states that the current flowing into a node must be equal to the current that flows out of the node.
+
!
Limits of KCL
+
⇨
Find KCL equation for one node
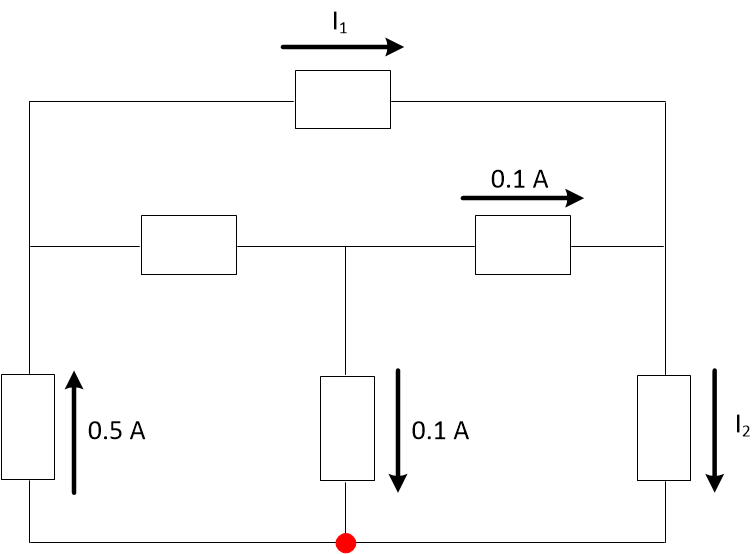
We want an equation that lets us solve for one of the currents we want. Preferably, this equation contains only one unknown.
We can apply KCL to the bottom node since we know all the currents that go in and out of that node except for \(I_2\).
We can apply KCL to the bottom node since we know all the currents that go in and out of that node except for \(I_2\).
\[0.5 \quad 0.1 \quad I_2\]
This will involve the 0.5 A, 0.1 A and \(I_2\) currents.
\[I_2 + 0.1 = 0.5\]
Current goes in on the left hand side, and goes out on the right hand side. This convention, of course, doesn't actually matter, but being consistent is a good way to avoid mistakes.
\[I_2 + 0.1 = 0.5\]
KCL expression for node at the bottom of the circuit.
★
\[I_2 = 0.4\]
Answer for Part 1
+
?
What about the unlabeled element?
Part 2
Find the second unknown current
+
⇨
Find KCL for second node
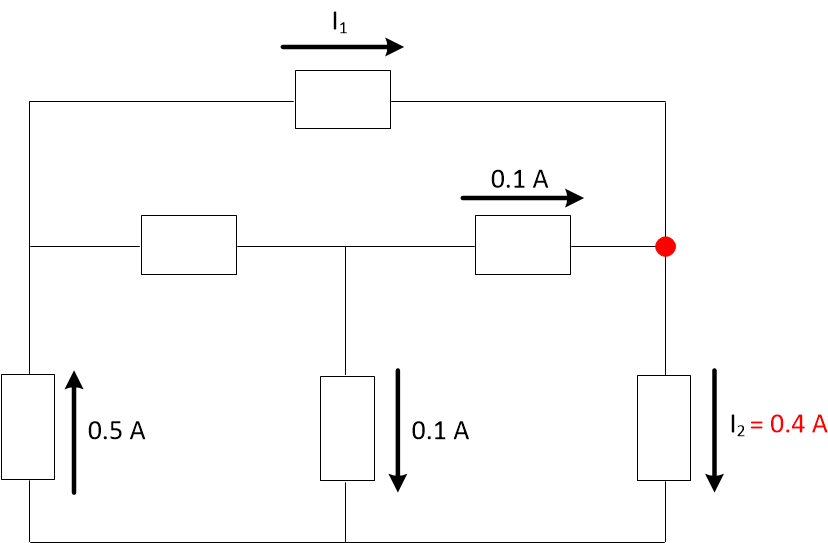
Now we can try to find another node to use and get \(I_1\). The node on the right is fine.
\[I_1 + 0.1 = I_2\]
Apply KCL. Current goes in on the left and out on the right
\[I_1 = I_2 - 0.1\]
Subtract 0.1 from both sides.
+
?
Why a variable?
We leave \(I_2\) as a variable at this step (even though we already know that it is \(0.4 \text{ A}\)) because if we had made a mistake, this way we can fix it faster.
\[I_1 = 0.4 - 0.1 = 0.3 \]
Substitute \(I_2 = 0.4 \)
★
\[I_1 = 0.3 \text{ A} \text{ and } I_2 = 0.4\text{ A}\]
Choice B was the correct answer
+
!
Alternate Node
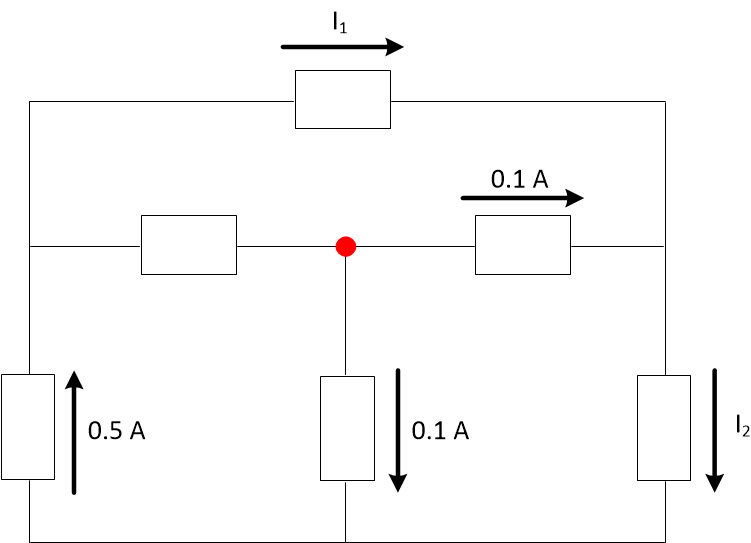
We could have used the central node to compute the current through the unlabeled element, and then used that to find \(I_1\). But we didn't, because that would be more work for us.


