Equivalent Resistance
Find the Equivalent Resistance between two terminals
Learn It!
Pre-Requisite Knowledge
To understand this section, you need to know the following concepts:
- Series and Parallel Resistors
- Circuit Transformation Rules
Goal
Equivalent Resistance
Find the Equivalent Resistance across terminals A & B and C & B
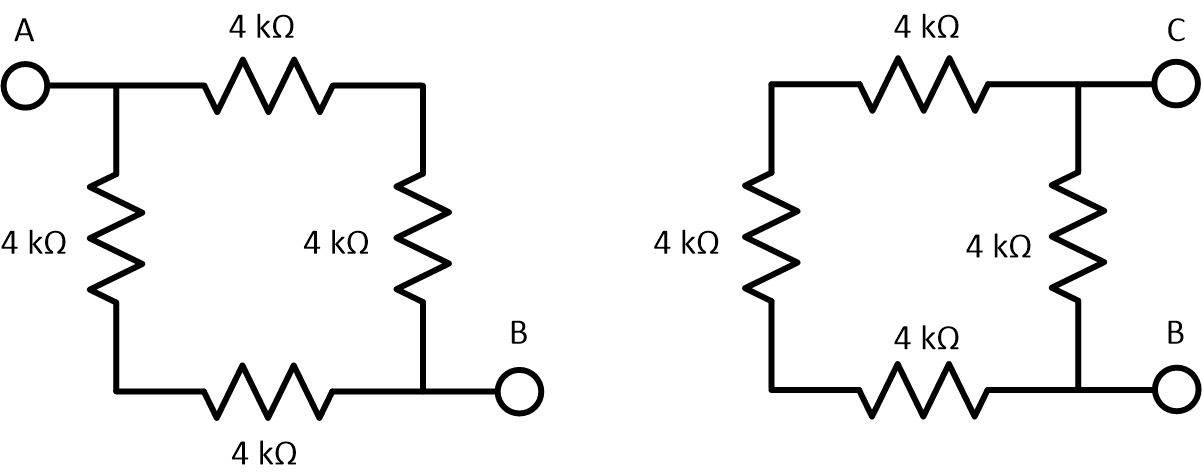
\(
\begin{equation}
a. R_{ab} = 8 k\Omega, R_{bc} = 4 k\Omega \\
b. R_{ab} = 4 k\Omega, R_{bc} = 8 k\Omega \\
c. R_{ab} = 4 k\Omega, R_{bc} = 3 k\Omega \\
d. R_{ab} = 3 k\Omega, R_{bc} = 8 k\Omega \\
e. R_{ab} = 3 k\Omega, R_{bc} = 3 k\Omega
\end{equation}
\)
Part 1
Reshape Both Circuits
The statement of the problem is straightforward, find the equivalent resistance. but The question seems at first a little absurd. It's the same resistors, why should the resistance be different?
It turns out they will be very different.
It turns out they will be very different.
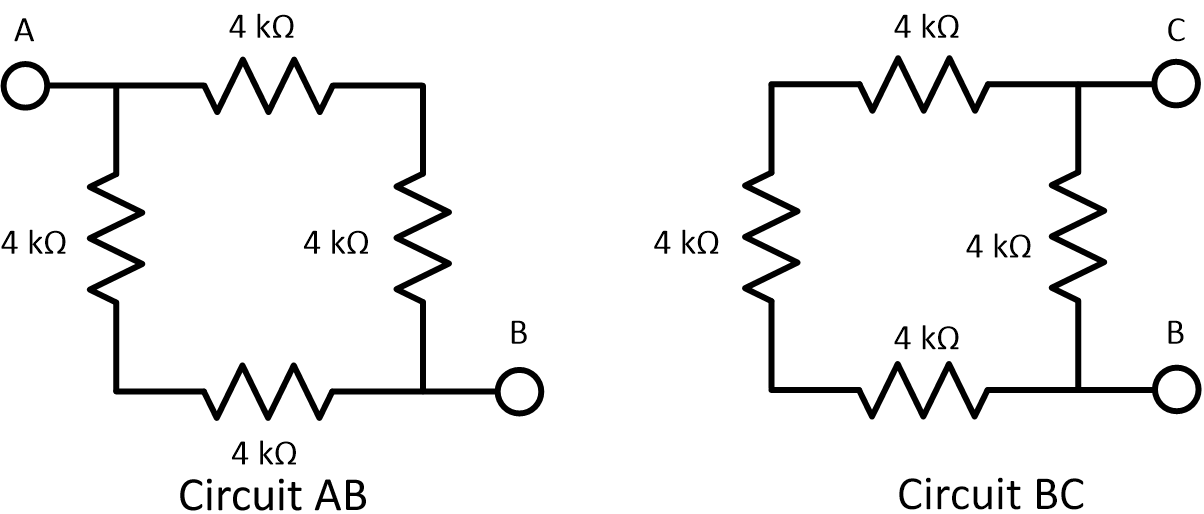
We start with two circuits that look very similar. I'll be refering to "Circuit AB" and "Circuit BC" to label the left and right circuits, respectively
+
1A
Transform both circuits
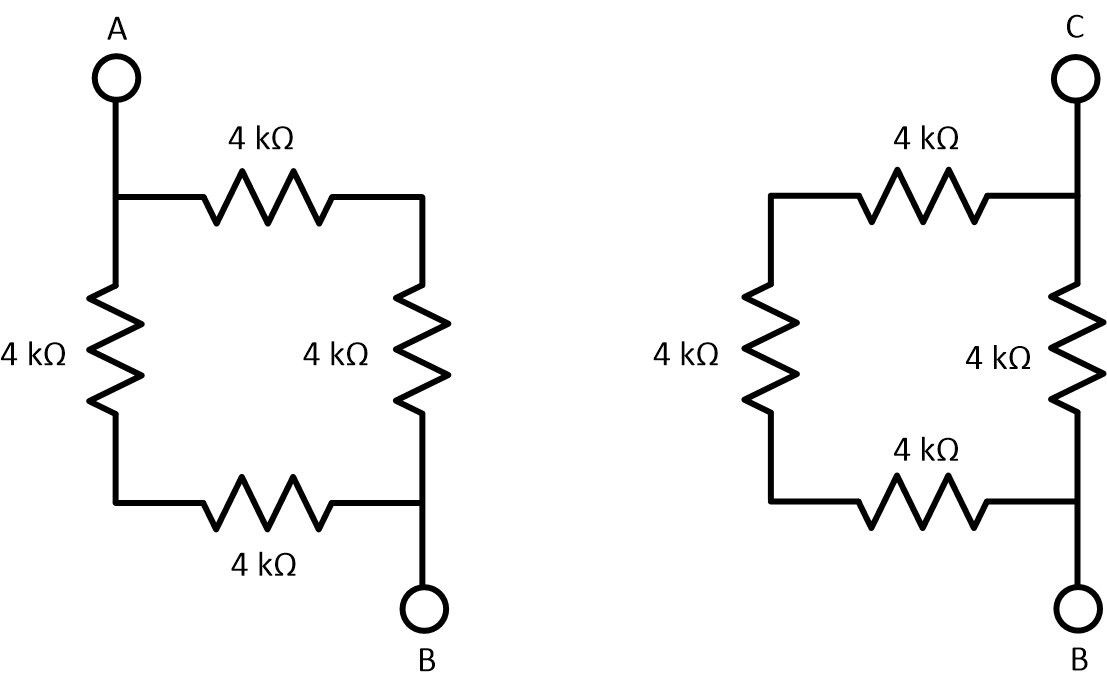
Let's slide the output terminals on both circuits around the corners to make them vertical.
Moving the terminals is usually one of the first steps when transforming a circuit
Moving the terminals is usually one of the first steps when transforming a circuit
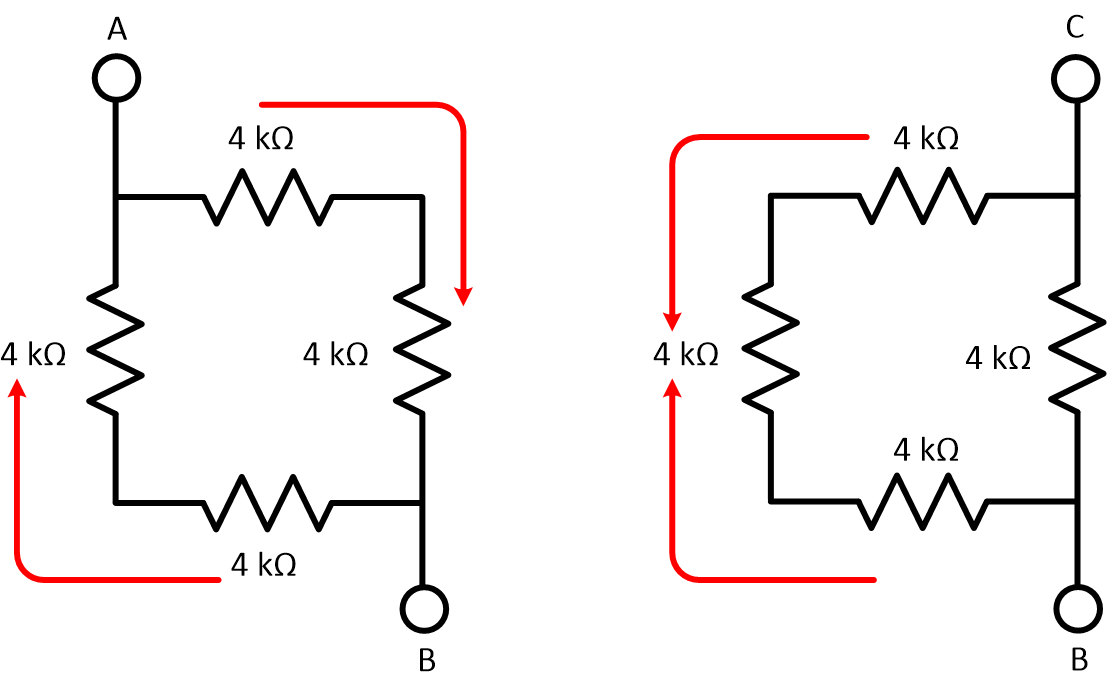
Next, we can slide the resistors around corners, getting them all vertical.
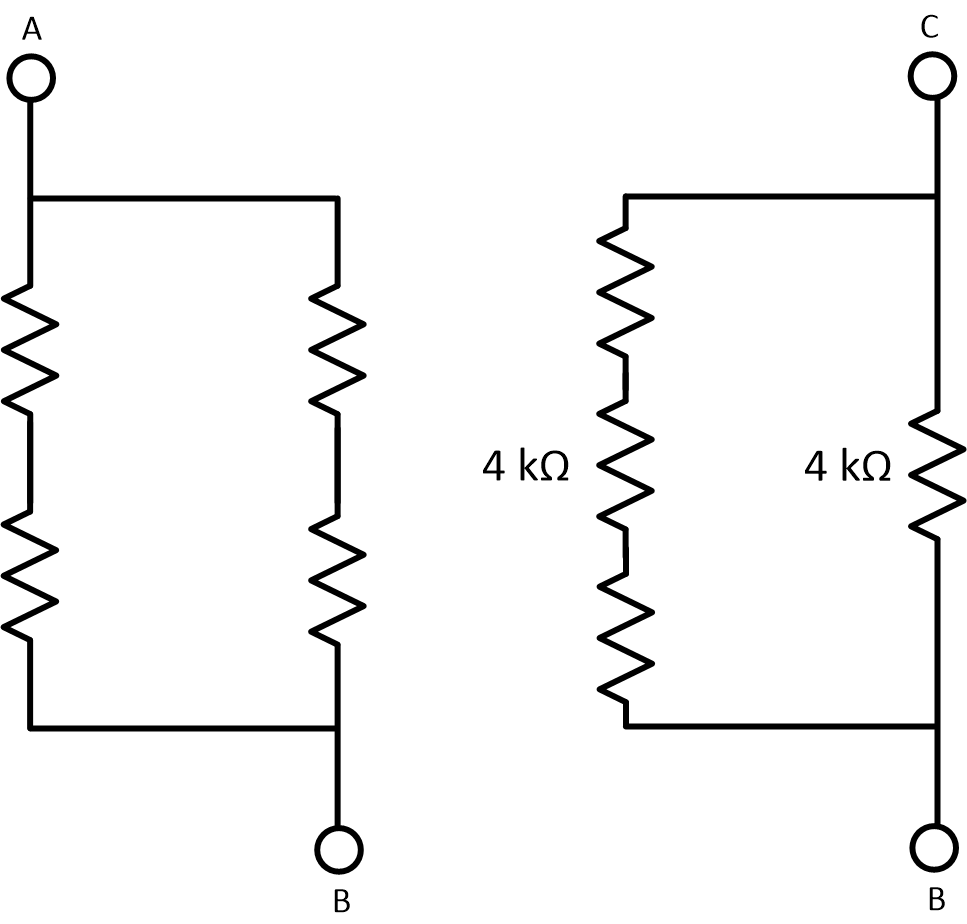
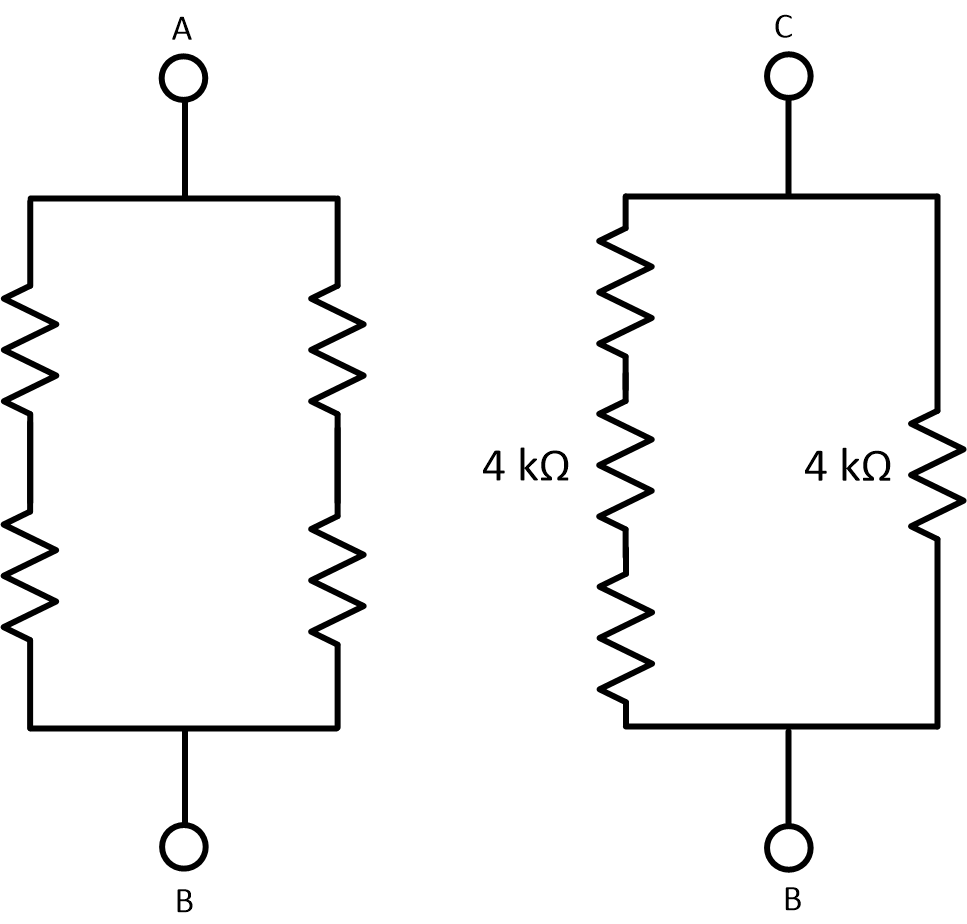
We can T-Slide the terminals over to the middle, now everything is immediately recognizable.
★

Fully Transformed
Part 2
Compute the Equivalent Resistance Using Formulas
\[R_{ab}=(R+R)||(R+R)\]
Circuit AB is two 2-resistor series configurations in parallel with each other.
\[R_{bc}=(R+R+R)||(R)\]
Circuit BC is a 3-resistor series in parallel with a single resistor.
+
2A
Reduce the circuits with series and parallel
\begin{align}
R_{ab}&=(2R)||(2R)\\
R_{bc}&=(3R)||(R)
\end{align}
Since the resistors are identical, we can simplify before applying the formulas
+
!
Abuse of Notation
What I just did is a bit of an abuse of notation. Which is the sign of good notation, that it can tolerate abuse and still give the right answer. "Abuse of notation" is not the same as "misuse of notation"
\begin{align}
R_{ab}&=\dfrac{1}{ \dfrac{1}{2R}+\dfrac{1}{2R}}\\
R_{bc}&=\dfrac{1}{ \dfrac{1}{3R}+\dfrac{1}{R}}
\end{align}
Apply parallel formulas. be careful not to lose a "one over" by accident.
\begin{aligned}
R_{ab}&=\dfrac{1}{ \dfrac{2}{2R}}=R&=4 \\
R_{bc}&=\dfrac{1}{ \dfrac{4}{3R}}= \dfrac{3}{4}R&=3
\end{aligned}
Simplify fractions.
★
\begin{align}
R_{ab}&=4 k\Omega \\
R_{bc}&=3 k\Omega
\end{align}
Final Answer
Equivalent resistance is not only a property of the resistor network, but also of what points you measure between.


