Voltage in a Circuit
Find the voltage of an element in a circuit
Learn It!
Pre-Requisite Knowledge
To understand this section, you need to know the following concepts:
Goal
Using the Voltage Divider Concept
Use the Voltage Divider concept to find the voltage drop across one resistor

\(
\begin{equation}
a. V_{out} = 1.5
\\b. V_{out} = 2V
\\c. V_{out} = 3V
\\d. V_{out} = 4.5V
\\e. V_{out} = 6V
\end{equation}
\)
Part 1
Using the Voltage Divider Rule
We want to find the voltage across the \(1 \Omega\) resistor, which has been named \(V_{out}\)
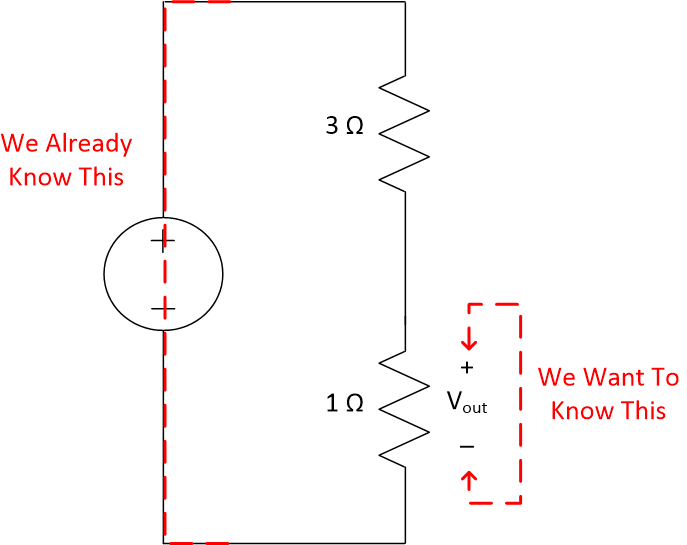
We recognize this as a special structure, called a voltage divider. If we want the voltage across one resistor that is in series with another, the voltage divider concept will likely be useful to us.
+
?
What about KVL and Ohm's Law?
+
!
Proof
\[V_1=V_{total} \frac{R_1}{R_1+R_2}\]
This is the Voltage Divider Rule (VDR).
The voltages across resistors in series have a this very special relationship.
The voltages across resistors in series have a this very special relationship.
\[V_{out}= 6\frac{1}{3+1}\]
With the VDR, we're on the home stretch.
★
\[V_{out} = 6/4 = 1.5\]
Final Answer is \(A\)


