Circuits
Adding an Element to a Circuit
Learn It!
Pre-Requisite Knowledge
To understand this section, you need to know the following concepts:
Goal
Analyzing Circuits
Add elements to a circuit and predict the effect on the other elements
In the circuit below, what happens to the brightness of the two light bulbs when the switch is closed, connecting the third light bulb to the circuit? You can assume that light bulbs are like resistors, and that a bulb's brightness is proportional to the current through it.
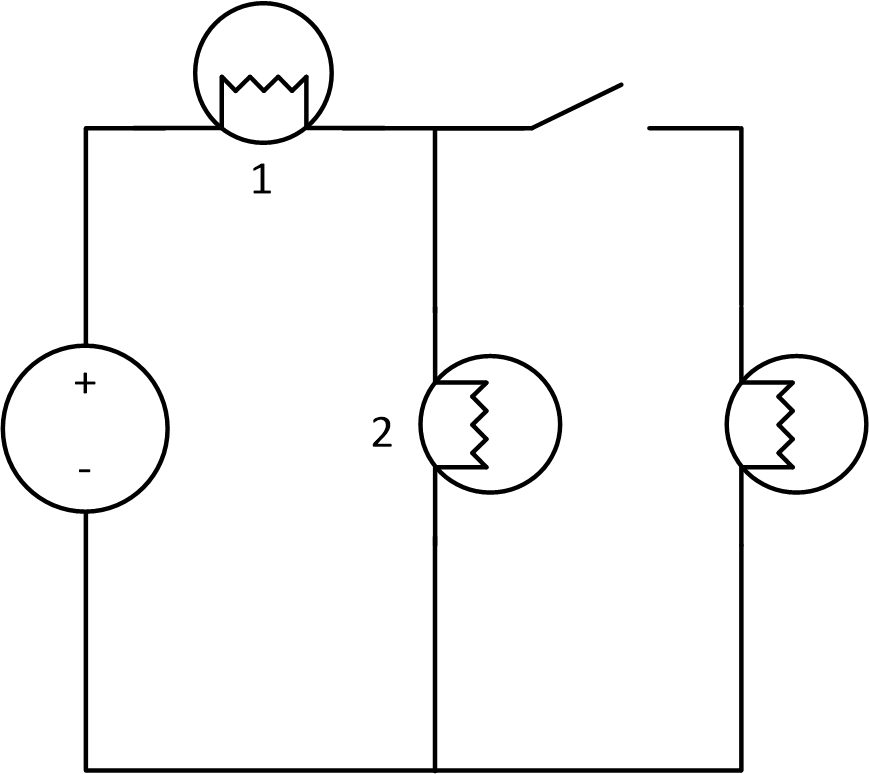
\(a.\) Bulbs 1 and 2 get brighter
\(b.\) Bulbs 1 and 2 get dimmer
\(c.\) Bulb 1 gets brighter and bulb 2 gets dimmer
\(d.\) Bulb 1 gets dimmer and bulb 2 gets brighter
\(e.\) Bulbs 1 and 2 stay the same
\(b.\) Bulbs 1 and 2 get dimmer
\(c.\) Bulb 1 gets brighter and bulb 2 gets dimmer
\(d.\) Bulb 1 gets dimmer and bulb 2 gets brighter
\(e.\) Bulbs 1 and 2 stay the same
Conceptual
Conceptual Analysis
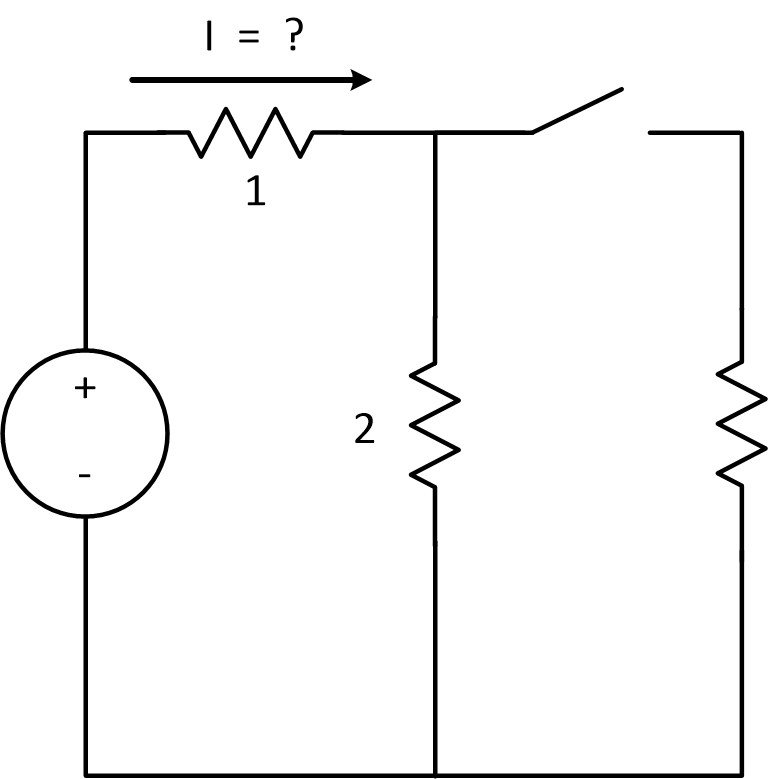
This is a conceptual problem, we don't have any numbers. We are told, however, that the bulbs act like resistors, and that brightness is proportional to the current. This means we can redraw our figure and start investigating what will happen.
We want to know about current, but we are given voltage (the source powering the bulbs). So we're not sure if VDR or CDR will help us just yet.
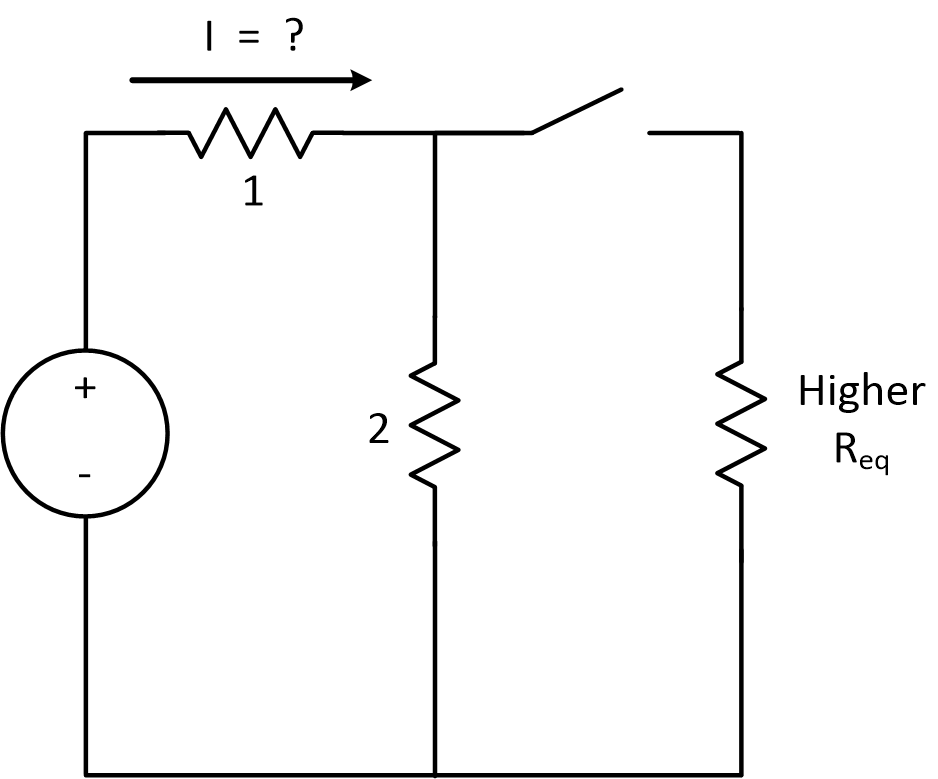
What has changed between these two states? We put in another resitor, so there was definitely a change in equivalent resistance.
We added another element in parallel with resistor 2. and we know that adding an element in parallel lowers resistance.
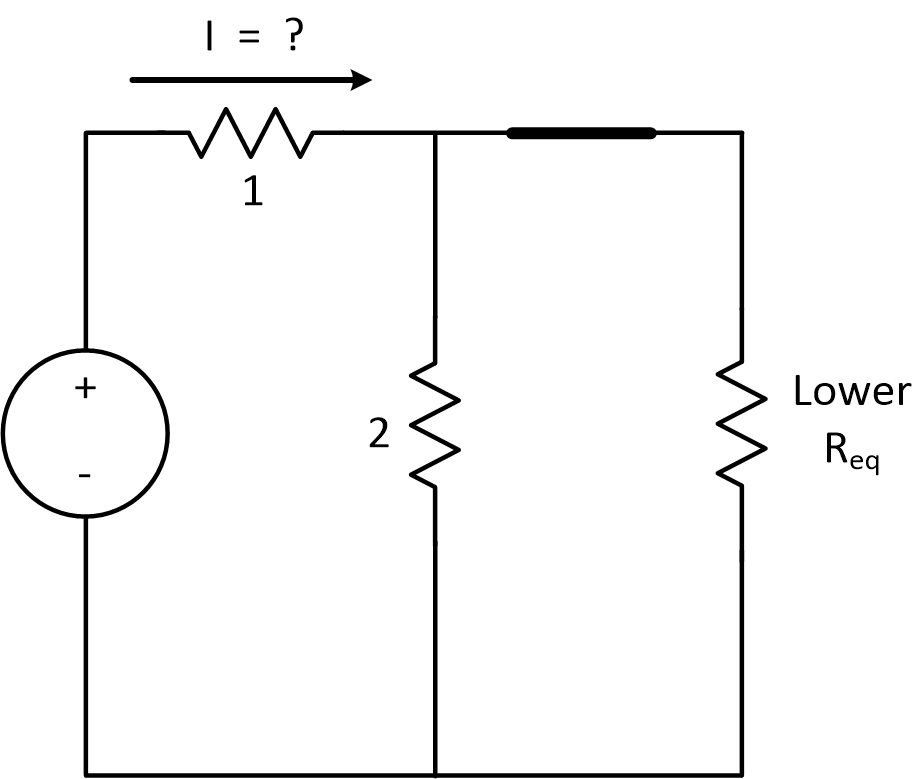
What has changed between these two states? We put in another resitor, so there was definitely a change in equivalent resistance.
We added another element in parallel with resistor 2. and we know that adding an element in parallel lowers resistance.
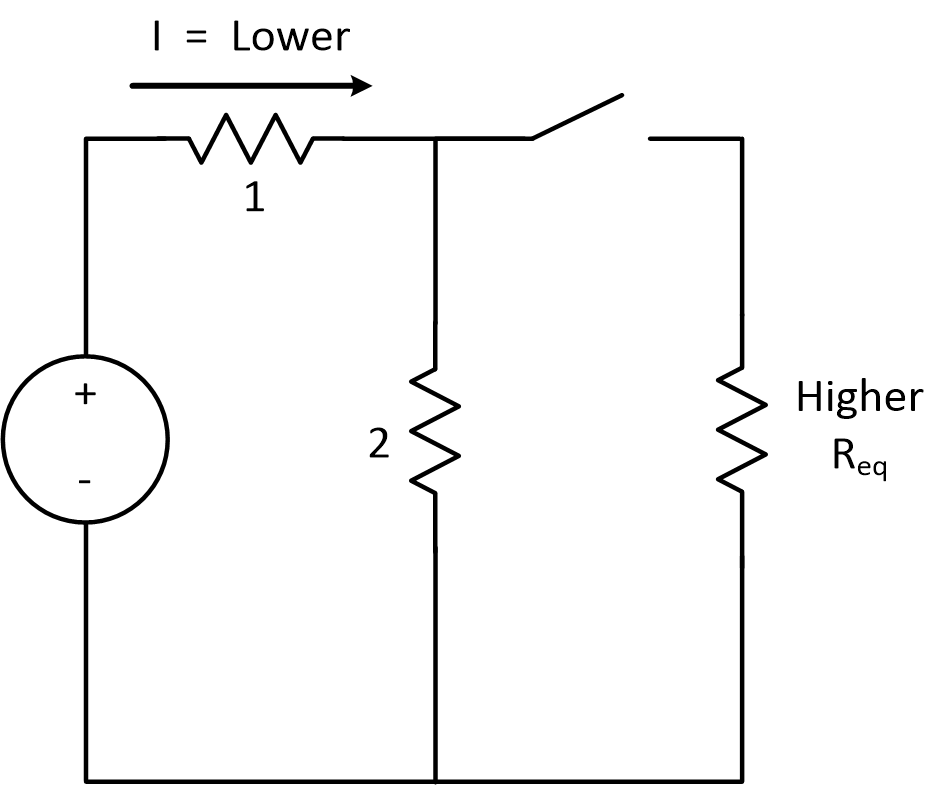
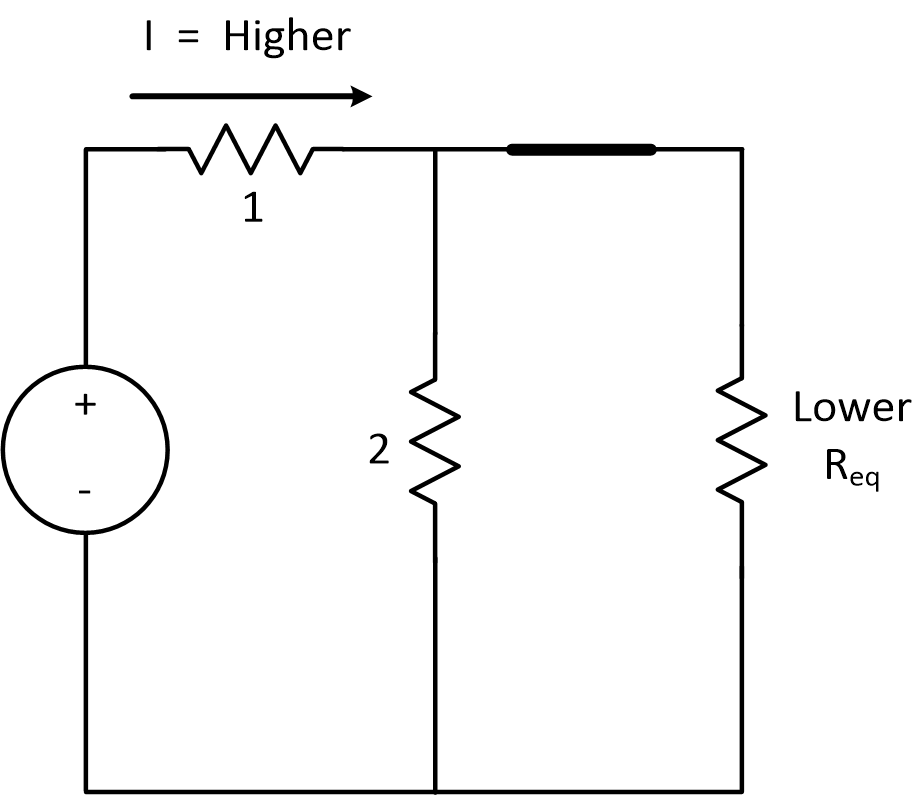
Since resistance was lowered, but voltage stayed the same, that means current has to rise to compensate.
the total current through the whole resistor network is equal to the current through element 1, since element 1 is in series with the rest of the circuit.
The current in element 1 rises, since the total current rose.
Bulb 1 gets brighter
This eliminates answers B, D, and E
the total current through the whole resistor network is equal to the current through element 1, since element 1 is in series with the rest of the circuit.
The current in element 1 rises, since the total current rose.
Bulb 1 gets brighter
This eliminates answers B, D, and E
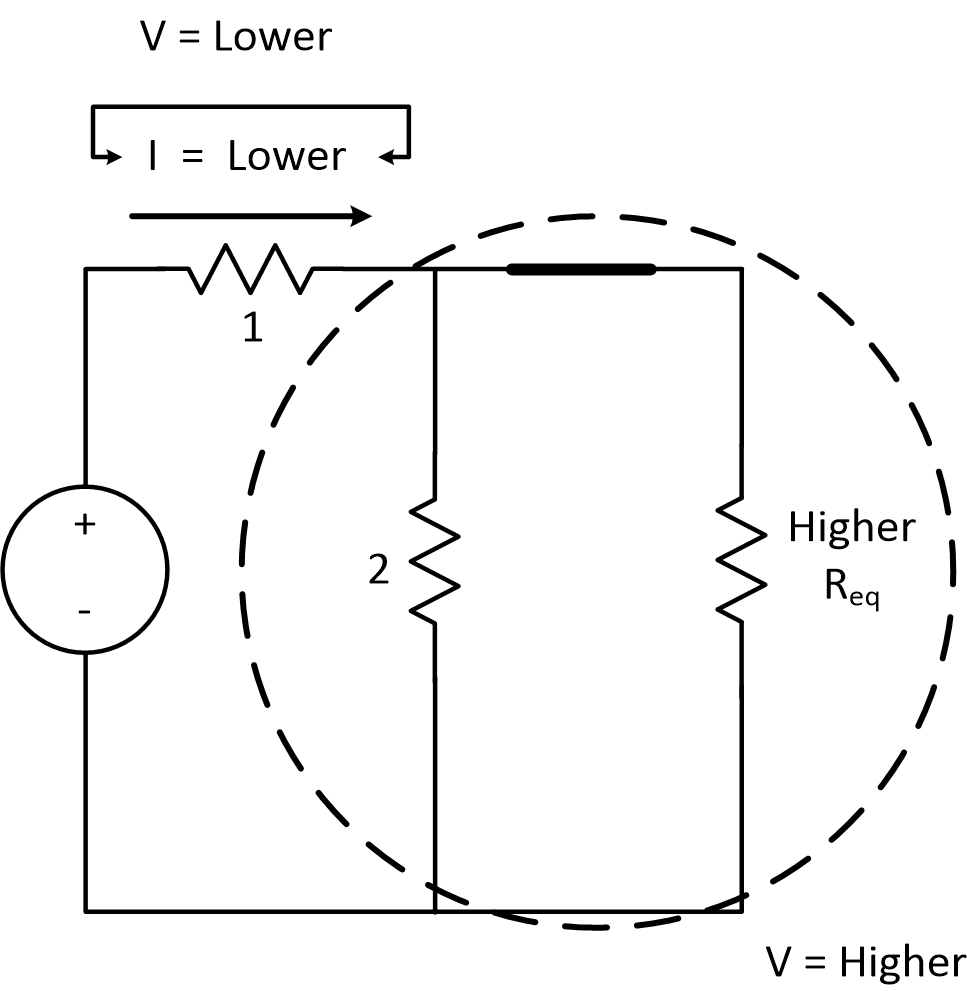
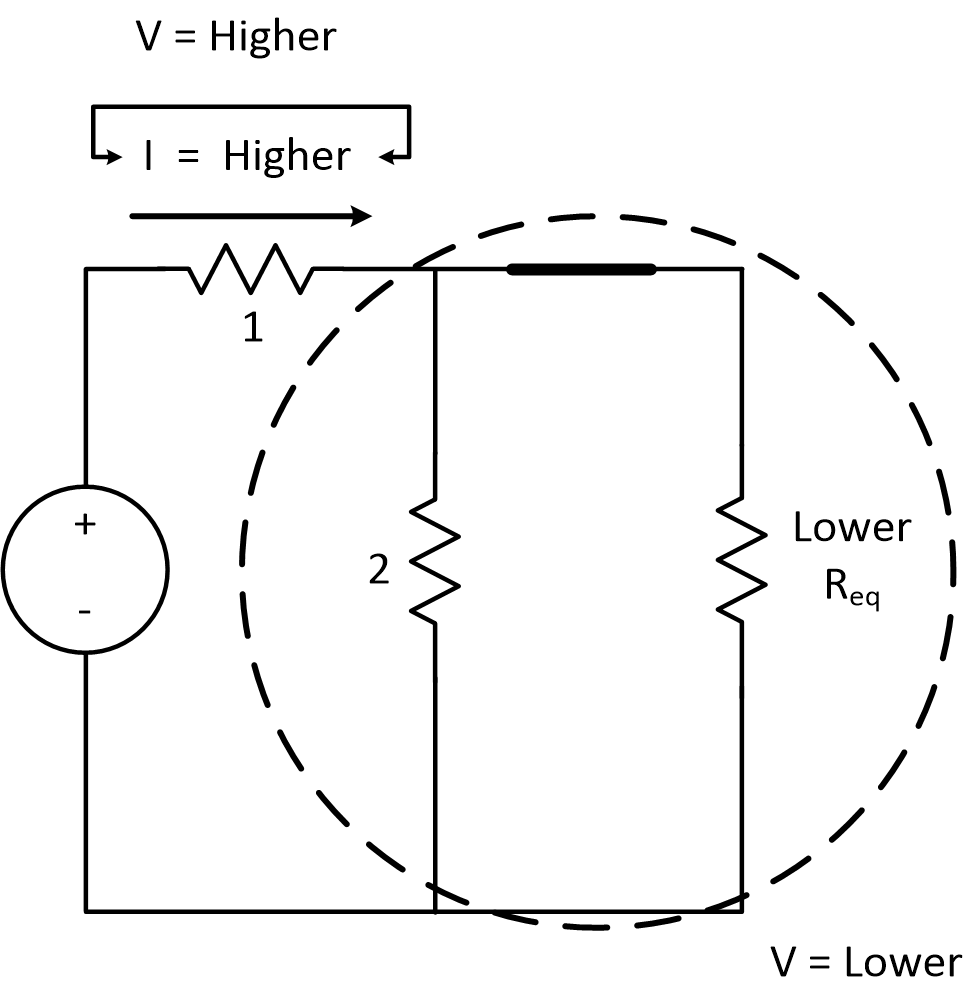
Now we have to figure out what happens to bulb 2 without knowing anything about the new resistance exept that it is positive
We found out in the previous section that element 1 has more current. This means, by Ohm's law, that it is also consuming more voltage.
If element 1 is consuming more voltage, then that means that the rest of the circuit (element 2 and the new element) must have a lower voltage drop than before, since the two must add up to the source in either case.
And resistor 2 is in a parallel configuration. The voltage across a parallel configuration is identical to the voltage across each of the elements. That voltage just dropped.
And with lower voltage comes lower current, and with lower current comes lower brightness.
Therefore, bulb 2 gets dimmer
We found out in the previous section that element 1 has more current. This means, by Ohm's law, that it is also consuming more voltage.
If element 1 is consuming more voltage, then that means that the rest of the circuit (element 2 and the new element) must have a lower voltage drop than before, since the two must add up to the source in either case.
And resistor 2 is in a parallel configuration. The voltage across a parallel configuration is identical to the voltage across each of the elements. That voltage just dropped.
And with lower voltage comes lower current, and with lower current comes lower brightness.
Therefore, bulb 2 gets dimmer
★
Bulb 2 gets dimmer
Answer for the problem
Mathematical
Mathematical analysis
For those unsatisfied with the conceptual analysis this is the full mathematical proof for the problem above.
As can be seen, the qualitative way of solving things can get us a small result, like 'increases' or 'decreases' for relatively little effort. To get exactly HOW MUCH it increases, we have to do some math. And by some math I mean a lot of tedious algebra.


