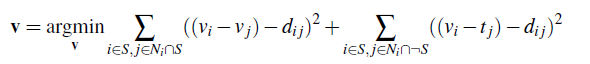Due Date: 11:59pm on Monday, Oct. 14, 2013
Overview
This project explores gradient-domain processing, a simple technique with a broad set of applications including blending, tone-mapping, and non-photorealistic rendering. For the core project, we will focus on "Poisson blending"; tone-mapping and NPR can be investigated as bells and whistles.
The primary goal of this assignment is to seamlessly blend an object or texture from a source image into a target image. The simplest method would be to just copy and paste the pixels from one image directly into the other. Unfortunately, this will create very noticeable seams, even if the backgrounds are well-matched. How can we get rid of these seams without doing too much perceptual damage to the source region?
The insight is that people often care much more about the gradient of an image than the overall intensity. So we can set up the problem as finding values for the target pixels that maximally preserve the gradient of the source region without changing any of the background pixels. Note that we are making a deliberate decision here to ignore the overall intensity! So a green hat could turn red, but it will still look like a hat.
We can formulate our objective as a least squares problem. Given the pixel intensities of the source image "s" and of the target image "t", we want to solve for new intensity values "v" within the source region "S":
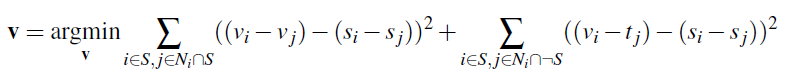
Here, each "i" is a pixel in the source region "S", and each "j" is a 4-neighbor of "i". Each summation guides the gradient values to match those of the source region. In the first summation, the gradient is over two variable pixels; in the second, one pixel is variable and one is in the fixed target region.
The method presented above is called "Poisson blending". Check out the Perez et al. 2003 paper to see sample results, or to wallow in extraneous math. This is just one example of a more general set of gradient-domain processing techniques. The general idea is to create an image by solving for specified pixel intensities and gradients.
Toy Problem (20 pts)
 The implementation for gradient domain processing is not complicated, but it is easy to make a mistake, so let's start with a toy example. Reconstruct this image from its gradient values, plus one pixel intensity. Denote the intensity of the source image at (x, y) as s(x,y) and the value to solve for as v(x,y). For each pixel, then, we have two objectives:
The implementation for gradient domain processing is not complicated, but it is easy to make a mistake, so let's start with a toy example. Reconstruct this image from its gradient values, plus one pixel intensity. Denote the intensity of the source image at (x, y) as s(x,y) and the value to solve for as v(x,y). For each pixel, then, we have two objectives:
1. minimize (v(x+1,y)-v(x,y) - (s(x+1,y)-s(x,y)))^2
2. minimize (v(x,y+1)-v(x,y) - (s(x,y+1)-s(x,y)))^2
Note that these could be solved while adding any constant value to v, so we will add one more objective:
3. minimize (v(1,1)-s(1,1))^2
For 20 points, solve this in Matlab as a least squares problem. If your solution is correct, then you should recover the original image.
Implementation Details
The first step is to write the objective function as a set of least squares constraints in the standard matrix form: (Av-b)^2. Here, "A" is a sparse matrix, "v" are the variables to be solved, and "b" is a known vector. It is helpful to keep a matrix "im2var" that maps each pixel to a variable number, such as:
[imh, imw, nb] = size(im);
im2var = zeros(imh, imw);
im2var(1:imh*imw) = 1:imh*imw;
Then, you can write objective 1 above as:
e=e+1;
A(e, im2var(y,x+1))=1;
A(e, im2var(y,x))=-1;
b(e) = s(y,x+1)-s(y,x);
Here, "e" is used as an equation counter. Note that the y-coordinate is the first index in Matlab convention. As another example, objective 3 above can be written as:
e=e+1;
A(e, im2var(1,1))=1;
b(e)=s(1,1);
To solve for v, use
v = A\b; or
v = lscov(A, b);
Then, copy each solved value to the appropriate pixel in the output image.
Poisson Blending (60 pts)
Step 1: Select source and target regions. Select the boundaries of a region in the source image and specify a location in the target image where it should be blended. Then, transform (e.g., translate) the source image so that indices of pixels in the source and target regions correspond. I've provided starter code (getMask.m, alignSource.m) to help with this. You may want to augment the code to allow rotation or resizing into the target region. You can be a bit sloppy about selecting the source region -- just make sure that the entire object is contained. Ideally, the background of the object in the source region and the surrounding area of the target region will be of similar color.
Step 2: Solve the blending constraints:
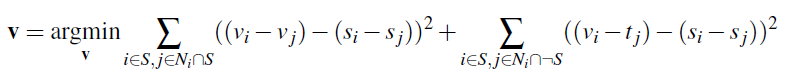
Step 3: Copy the solves values into your target image. For RGB images, process each channel separately. Show at least three results of Poisson blending. Explain any failure cases (e.g., weird colors, blurred boundaries, etc.).
Tips
1. Initialize your sparse matrix with
sparse([], [], [], M, N, nzmax)
for a matrix with M equations and N variables and at most nzmax non-zero entries.
2. Before trying new examples, try something that you know should work, such as the included penguins on top of the snow in the hiking image.
3. Object region selection can be done very crudely, with lots of room around the object.
Mixed Gradients (20 pts)
Follow the same steps as Poisson blending, but use the gradient in source or target with the larger magnitude as the guide, rather than the source gradient:
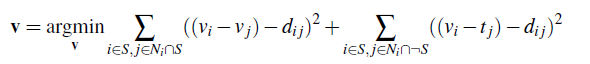
Here "d_ij" is the value of the gradient from the source or the target image with larger magnitude. Note that larger magnitude is not the same as greater value. For example, if the two gradients are -0.6 and 0.4, you want to keep the gradient of -0.6. Show at least one result of blending using mixed gradients. One possibility is to blend a picture of writing on a plain background onto another image.
Bells & Whistles (Extra Points)
Color2Gray (20 pts)
Sometimes, in converting a color image to grayscale (e.g., when printing to a laser printer), we lose the important contrast information, making the image difficult to understand. For example, compare the color version of the image on right with its grayscale version produced by rgb2gray.


Can you do better than rgb2gray? Gradient-domain processing provides one avenue: create a gray image that has similar intensity to the rgb2gray output but has similar contrast to the original RGB image. This is an example of a tone-mapping problem, conceptually similar to that of converting HDR images to RGB displays. To get credit for this, show the grayscale image that you produce (the numbers should be easily readable) and include your code in the e-mailed zip.
Hint: Try converting the image to HSV space and looking at the gradients in each channel. Then, approach it as a mixed gradients problem where you also want to preserve the grayscale intensity.
Laplacian pyramid blending (20 pts)
Another technique for blending is to decompose the source and target images using a laplacian pyramid and to combine using alpha mattes. For the low frequencies, there should be a slow transition in the alpha matte from 0 to 1; for the high frequencies, the transition should be sharp. Try this method on some of your earlier results and compare to the Poisson blending.
More gradient domain processing (up to 20 pts)
Many other applications are possible, including non-photorealistic rendering, edge enhancement, and texture or color transfer. See Perez et al. 2003 or Gradient Shop for further ideas.
Materials
- Images, including the toy image, sample images for blending, and the color2gray image.
- Starter Code, including a top-level script and functions to select the source region and align source and target images for blending.
Deliverables
To turn in your assignment, place your index.html file and any supporting media in your project directory: http://web.engr.illinois.edu/~netid/cs498dwh/proj3/, where "netid" is your netid (e.g., dhoiem). Also, e-mail me the zipped code in "netid_proj3.zip" and include a link to the project page in the text. See project instructions for details. In the e-mail, tell me how many points you think you should get for the core project and any bells and whistles.
Use both words and images to show us what you've done. Please:
-
Show your favorite blending result. Include: 1) the source and target image; 2) the blended image with the source pixels directly copied into the target region; 3) the final blend result. Briefly explain how it works, along with anything special that you did or tried. This should be with your own images, not the included samples.
-
Next, show at least two more results for Poisson blending, including one that doesn't work so well (failure example).
Explain any difficulties and possible reasons for bad results.
-
Show at least one result for blending with mixed gradients. Again, show the source image, target image, and final result.
-
Include code for poisson blending, mixed gradients, and the toy reconstruction problem. It should be clear from the filenames which is which (e.g., "poisson.m, mixed.m, toy.m"). You do not need to show the reconstructed toy image (everyone's should look the same), but do include the code and report the root-mean-squared (RMS) error, which the starter code will print.
- Describe and bells and whistles under a separate heading and include relevant code.
Scoring
The core assignment is worth 100 points, as follows:
- 20 points for implementation of toy image reconstruction.
- 60 points for Poisson blending implementation, results, and description: 30 pts for first result; 20 points for additional two (or more) results; 10 points for clarity of presentation.
- 20 points for mixed gradients implementation and at least one result.
You can also earn up to 60 extra points for the bells & whistles mentioned above
(20 for color2gray; 20 for comparison to pyramid blending; up to 20 for additional gradient domain processing applications.
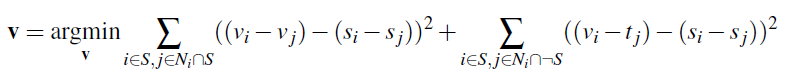

 The implementation for gradient domain processing is not complicated, but it is easy to make a mistake, so let's start with a toy example. Reconstruct this image from its gradient values, plus one pixel intensity. Denote the intensity of the source image at (x, y) as s(x,y) and the value to solve for as v(x,y). For each pixel, then, we have two objectives:
The implementation for gradient domain processing is not complicated, but it is easy to make a mistake, so let's start with a toy example. Reconstruct this image from its gradient values, plus one pixel intensity. Denote the intensity of the source image at (x, y) as s(x,y) and the value to solve for as v(x,y). For each pixel, then, we have two objectives: