Homework 1: Classification With Naive Bayes
About
Due
Monday 1/28/19, 11:59 PM CST (AML)
Thursday 1/31/19, 11:59 PM CST (AMO*)
* AMO students are allowed a 3-day extension due to the late release of the AMO Coursera materials. (Updated on 1/18)
Goal
This homework focuses on classification using simple naive Bayes and decision forest classifiers.
Additionally, it is intended to provide practice with finding and using publicly available libraries, an essential skill when applying machine learning techniques.
Submission
Submission will be through gradescope:
1. Login to gradescope with your UI email, click "Enroll in Course" on right bottom with the entry code mailed to you.
2. Choose the course, and in the dashboard page, click HW1.
3. Then click "Upload Submission" on right bottom. It's allowed for multiple submissions before the due date.
4. AMO students are granted for 3 days extension so late submissions before 1/31 are allowed. (Write CS498 AMO on the first page for clarity)
Code and External Libraries
The assignment can be done using any programming language. Python is recommended.
External libraries can be used for all part of the assignment except where specifically mentioned below.
Problems
Total points: 100
Problem 1: Diabetes Classification
Points: 40
A famous collection of data on whether a patient has diabetes, known as the Pima Indians dataset, and originally owned by the National Institute of Diabetes and Digestive and Kidney Diseases can be found at Kaggle. Download this dataset from https://www.kaggle.com/kumargh/pimaindiansdiabetescsv. This data has a set of attributes of patients, and a categorical variable telling whether the patient is diabetic or not. For several attributes in this data set, a value of 0 may indicate a missing value of the variable. There are a total of 767 data-points.
Part 1A
Build a simple naive Bayes classifier to classify this data set. You should use a normal distribution to model each of the class-conditional distributions.
- Compute an estimate of the accuracy of the classifier by averaging over 10 test-train splits. Each split should randomly assign 20% of the data to test, and the rest to train.
You should write this classifier and the test-train split code yourself (it's quite straight-forward). Libraries can be used to load & hold the data.
Part 1B
Now adjust your code so that, for attribute 3 (Diastolic blood pressure), attribute 4 (Triceps skinfold thickness), attribute 6 (Body mass index), and attribute 8 (Age), it regards a value of 0 as a missing value when estimating the class-conditional distributions, and the posterior.
- Compute an estimate of the accuracy of the classifier by averaging over 10 test-train splits.
Problem 2: MNIST Image Classification
Points: 60
The MNIST dataset is a dataset of 60,000 training and 10,000 test examples of handwritten digits, originally constructed by Yann Lecun, Corinna Cortes, and Christopher J.C. Burges. It is very widely used to check simple methods. There are 10 classes in total ("0" to "9"). This dataset has been extensively studied, and there is a history of methods and feature constructions at https://en.wikipedia.org/wiki/MNIST_database and at the original site, http://yann.lecun.com/exdb/mnist/. You should notice that the best methods perform extremely well.
(Updated 1/19) The http://yann.lecun.com/exdb/mnist/ dataset is stored in an unusual format, described in detail on the page. You do not have to write your own reader. A web search should yield solutions for both Python and R. For Python, https://pypi.org/project/python-mnist/ should work. For R, there is reader code available at https://stackoverflow.com/questions/21521571/how-to-read-mnist-database-in-r. Please note that if you follow the recommendations in the accepted answer there at https://stackoverflow.com/a/21524980, you must also provide the readBin call with the flag signed=FALSE since the data values are stored as unsigned integers.
The dataset consists of 28 x 28 images. These were originally binary images, but appear to be grey level images as a result of some anti-aliasing. I will ignore mid-grey pixels (there aren't many of them) and call dark pixels "ink pixels", and light pixels "paper pixels"; you can modify the data values with a threshold to specify the distinction, as described here https://en.wikipedia.org/wiki/Thresholding_(image_processing). The digit has been centered in the image by centering the center of gravity of the image pixels, but as mentioned on the original site, this is probably not ideal. Here are some options for re-centering the digits that I will refer to in the exercises.
- Untouched: Do not re-center the digits, but use the images as is.
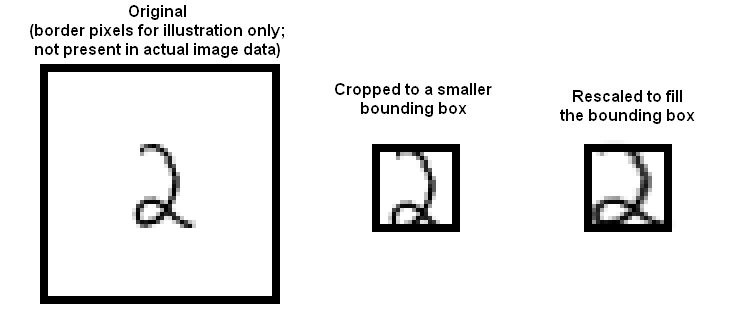
- Bounding box: Construct a 20 x 20 bounding box so that the horizontal (resp. vertical) range of ink pixels is centered in the box.
- Stretched bounding box: Construct a 20 x 20 bounding box so that the horizontal (resp. vertical) range of ink pixels runs the full horizontal (resp. vertical) range of the box. Obtaining this representation will involve rescaling image pixels: you find the horizontal and vertical ink range, cut that out of the original image, then resize the result to 20 x 20. Once the image has been re-centered, you can compute features.
- Here are some pictures, which may help
Part 2A: MNIST using naive Bayes
Model each class of the dataset using a Normal distribution and (separately) a Bernoulli distribution for both untouched images v. stretched bounding boxes, using 20 x 20 for your bounding box dimension. This should result in 4 total models. Use the training set to calculate the distribution parameters.
You must write the naive Bayes prediction code. The distribution parameters can be calculated manually or via libraries. Additionally, we recommend using a library to load the MNIST data (e.g. python-mnist or scikit-learn) and to rescale the images (e.g. openCV).
- Compute the accuracy values for the four combinations of Normal v. Bernoulli distributions for both untouched images v. stretched bounding boxes. Both the training and test set accuracy will be reported.
- For each digit, plot the mean pixel values calculated for the Normal distribution of the untouched images. In Python, a library such as matplotlib should prove useful.
Part 2B: MNIST using Decision Forest
- Classify MNIST using a decision forest.
For your forest construction, you should investigate four cases. Your cases are: number of trees = (10, 30) X maximum depth = (4, 16). You should compute your accuracy for each of the following cases: untouched raw pixels; stretched bounding box. This yields a total of 8 slightly different classifiers. Please use 20 x 20 for your bounding box dimensions.
You should use a decision forest library. No need to write your own.
Submission
Your submission should be a PDF with the following pages.
Page 1
Part 1 Accuracies (10 points)
| Setup | Cross-validation Accuracy |
|---|---|
| Unprocessed data | ??? |
| 0-value elements ignored | ??? |
Page 2
Part 1 Code Snippets (30 points)
The page should contain snippets of code demonstrating:
- Calculation of distribution parameters
- Calculation of naive Bayes predictions
- Test-train split code
This should be a maximum of one page. If additional space is needed, please reference the full code you will attach to the end of the submission.
Page 3
Part 2 MNIST Accuracies (20 points)
| x | Method | Training Set Accuracy | Test Set Accuracy |
|---|---|---|---|
| 1 | Gaussian + untouched | ||
| 2 | Gaussian + stretched | ||
| 3 | Bernoulli + untouched | ||
| 4 | Bernoulli + stretched | ||
| 5 | 10 trees + 4 depth + untouched | ||
| 6 | 10 trees + 4 depth + stretched | ||
| 7 | 10 trees + 16 depth + untouched | ||
| 8 | 10 trees + 16 depth + stretched | ||
| 9 | 30 trees + 4 depth + untouched | ||
| 10 | 30 trees + 4 depth + stretched | ||
| 11 | 30 trees + 16 depth + untouched | ||
| 12 | 30 trees + 16 depth + stretched |
Page 4
Part 2A Digit Images (10 points)
| Digit | Mean Image |
|---|---|
| 0 | ??? |
| 1 | ??? |
| 2 | ??? |
| 3 | ??? |
| 4 | ??? |
| 5 | ??? |
| 6 | ??? |
| 7 | ??? |
| 8 | ??? |
| 9 | ??? |
Page 5
Part 2 Code (30 points)
The page should contain snippets of code demonstrating:
- Calculation of the Normal distribution parameters
- Calculation of the Bernoulli distribution parameters
- Calculation of the Naive Bayes predictions
- Training of a decision tree
- Calculation of a decision tree predictions
This should be a maximum of one page. If additional space is needed, please reference the full code you will attach to the end of the submission.
Page 6+
All code should be attached at the end of the pdf. There is no limit to the number of pages required for full code printout.