Make it easy for the graders to figure out what you mean in the short time they have to grade your solution. If your solutions are difficult to read or understand, you will lose points (and the graders will be less sympathetic to your other mistakes).
Be Clear
- Write carefully. We can only grade what you actually write, not what you mean. We will not attempt to read your mind. If your answer is ambiguous, we will deliberately choose the interpretation that makes it wrong.
- Write legibly. If we can't decipher your solution, we can't give you credit. If you have sloppy handwriting, use LaTeX. Please don't submit your first draft.
- Write sensibly. You will lose points for poor spelling, grammar, punctuation, arithmetic, algebra, logic, and so on. This rule is especially important for students whose first language is not English.
- Give generic solutions, not just examples. In particular, don't describe the first two or three iterations of your algorithm and then write "and so on". Solutions that include phrases like “and so on”, “etc.”, “do this for all X”, or “. . .” will get no credit. Those phrases indicate precisely where you should have used iteration, recursion, or induction but didn’t.
- Make the punchline obvious. Emphasize key points (for example, running times) by putting a box around them, using a highlighter, or something similar.
- Write top-down, breadth-first solutions. Describe the key ideas behind your solution before going into details. The reader should understand your approach almost immediately. A clearly written solution that includes all the main ideas but omits some low-level details is worth more than a complete, correct, detailed, but opaque solution.
- State your assumptions. If a problem statement is ambiguous, explicitly state any additional assumptions that your solution requires. (Please also ask for clarification in class, in office hours, or on Piazza!) For example, if the performance of your algorithm depends on how the input is represented, tell us exactly what representation you require.
- Don't submit code. Describe your algorithms using clean, human-readable pseudocode. Your description should allow a competent programmer who has not taken this course to easily implement your algorithm in their favorite language.
Penn and Teller get 25%
Be Concise
- Keep it short. Every homework problem can be answered completely in at most two typeset pages or five handwritten pages; most problems require considerably less.
- Omit irrelevant details. Don't turn in the piece of paper you used to figure out your answer; copy the relevant information onto a new empty page. Don't write "red-black tree" when you mean "balanced binary tree" or "dictionary".
- Don't regurgitate. If your answer is similar to something we've seen in class, just say so and (carefully!) describe your changes. Vomiting will cost you points. For example, if the solution appears on page 6 of Jeff's notes, just write "See page 6 of Jeff's notes." Similarly, don't explain binary search; just write "binary search".
-
Don't bullshit. If you don't know the answer, just say so. Answering “I don't know” (and nothing else) is worth 25% partial credit. The "I don't know" rule applies to every problem and sub-problem (except extra credit problems) on every homework and exam. Synonyms like “No idea” or “WTF” or "
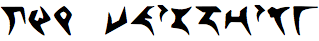 " are acceptable substitutes, but you must write something; a blank page is worth zero points. Readable, correct, but suboptimal solutions are always worth more than 25%.
" are acceptable substitutes, but you must write something; a blank page is worth zero points. Readable, correct, but suboptimal solutions are always worth more than 25%.
- Don't submit code. We want to see your ideas, not syntactic sugar.
Be Honest
- Write everything in your own words, and properly cite every outside source you use. We strongly encourge you to use any outside source at your disposal, provided you use your sources properly and give them proper credit. If you get an idea from an outside source, citing that source will not lower your grade. Failing to properly cite an outside source—thereby taking credit for ideas that are not your own—is plagiarism. The only sources that you are not required to cite are the official course materials (lectures, lecture notes, previous homework and exam solutions from this semester) and sources for prerequisite material (which we assume you already know by heart).
- List everyone you worked with on each homework problem. Again, we strongly encourage you to work together, but you must give everyone proper credit. If you work in a group of 20 students, then all 20 names should appear on your homework solution. If someone was particularly helpful, describe their contribution. Be generous; if you're not sure whether someone should be included in your list of collaborators, include them. For discussions in class, in section, or in office hours, where collecting names is impractical, it's okay to write something like "discussions in class".
- Please see our academic integrity policy for more details.
Content: What to write
You're gonna start a fight and you're gonna lose.
- Answer the right question. No matter how clear and polished your solution is, it's worthless if it doesn't answer the question we asked. Make sure you understand the question before you start thinking about how to answer it. If something is unclear, ask for clarification! This is especially important on exams.
- Justify your answers. Unless the problem specifically says otherwise, every homework problem requires a proof. Without a proof, even a perfectly correct solution is worth nothing. In particular, the sentence "It's obvious!" is not a proof—'obvious' is often a synonym for 'false'! However, proofs are only required on exams if we specifically ask for them.
-
By default, if a homework or exam problem asks you to describe an algorithm, you need to do several things to get full credit:
- If necessary, formally restate the problem in terms of combinatorial objects such as sets, sequences, lists, graphs, or trees. In other words, tell us what the problem is really asking for. This is often the hardest part of designing an algorithm.
- Give a concise pseudocode description of your algorithm. Don't regurgitate, and don't turn in code!
- Describe a correct algorithm.
- Justify the correctness of your algorithm. You usually won't have to do this on exams.
- Analyze your algorithm's running time. This may be as simple as saying "There are two nested loops from 1 to n, so the running time is O(n²)." Or it may require setting up and solving a summation and/or a recurrence, in which case you'll also have to prove your answer is correct.
- Describe the fastest correct algorithm you can, even if the problem does not include the words "fast" or "efficient". Faster algorithms are worth more points; brute force is usually not worth much. We will not always tell you what time bound to shoot for; that's part of what you're trying to learn. However, if your algorithm is incorrect, you won't get any points, no matter how fast it is!
Some problems may deviate from these default requirements. For example, we may ask you for an algorithm that uses a particular approach, even though another approach may be more efficient. (Answer the right question!) Some problems may ask you to analyze the space used by your algorithm in addition to the running time.
You're gonna start a fight and you're gonna lose.
- If necessary, formally restate the problem in terms of combinatorial objects such as sets, sequences, lists, graphs, or trees. In other words, tell us what the problem is really asking for. This is often the hardest part of designing an algorithm.
- Give a concise pseudocode description of your algorithm. Don't regurgitate, and don't turn in code!
- Describe a correct algorithm.
- Justify the correctness of your algorithm. You usually won't have to do this on exams.
- Analyze your algorithm's running time. This may be as simple as saying "There are two nested loops from 1 to n, so the running time is O(n²)." Or it may require setting up and solving a summation and/or a recurrence, in which case you'll also have to prove your answer is correct.
- Describe the fastest correct algorithm you can, even if the problem does not include the words "fast" or "efficient". Faster algorithms are worth more points; brute force is usually not worth much. We will not always tell you what time bound to shoot for; that's part of what you're trying to learn. However, if your algorithm is incorrect, you won't get any points, no matter how fast it is!