A Friendly Warning This lab has been designed to heavily depend upon the material taught in lab. Unless you feel pretty confident with network flow, it is highly advised not to start this lab without first attending your lab section.
Assignment Description
In this lab you will learn about:
- Flow in a network (a graph-oriented structure) and how to calculate it
- Residual graphs
Working with partners
For this lab since you will be working in groups of three people, we will allow you to write all of those people in your partners.txt file and you may work on the code with them as well. Alternatively you still have the option to work with someone that wasn’t in your group but you will be limited to only having that one person in your partners.txt file.
Lab Insight
Flow algorithms are very powerful and used for many things in the field of Computer Science. It is helpful many times to represent a system as a graph and the flow throughout that graph could very important. For example, flow algorithms are used all the time in networking to try to determine how much throughput a system is getting and whether there is a bottle neck. If you would like to learn more about some the applications for flow with respect to Networking, Distributed Systems, or Algorithms, look into CS 438, CS 425, and CS 473 respectively
Checking Out The Code
Get the code in the usual way.
From your CS 225 git directory, run the following on EWS:
git fetch release
git merge release/lab_flow -m "Merging initial lab_flow files"
If you’re on your own machine, you may need to run:
git fetch release
git merge --allow-unrelated-histories release/lab_flow -m "Merging initial lab_flow files"
Graph Class
In this lab, you will make use of a graph class that we have implemented for you. With this graph class you
will need to insert a directional edge, which goes from a source vertex to a destination vertex. The Edge
class is defined for you in edge.h and we define the structure Vertex to just be a string.
It is recommended that you read up on the graph class and it’s API, see the Doxygen for this lab
(or check out the file graph.h).
Network Flow
The idea behind a network flow is to use graph entities to model a sort of capacity problem along various paths. Basically, flow is bounded by the edge weights in a graph. As we compute the total graph flow, we build a secondary residual graph to keep track of the remaining capacity of the edges in the graph.
When we begin calculating flow through a network, we build a residual graph to aid us. The residual graph keeps track of the remaining capacity each edge currently supports. When we begin our algorithm we set the flow on all edges to 0 and we assign the weights of our edges to the residual graph like show below.
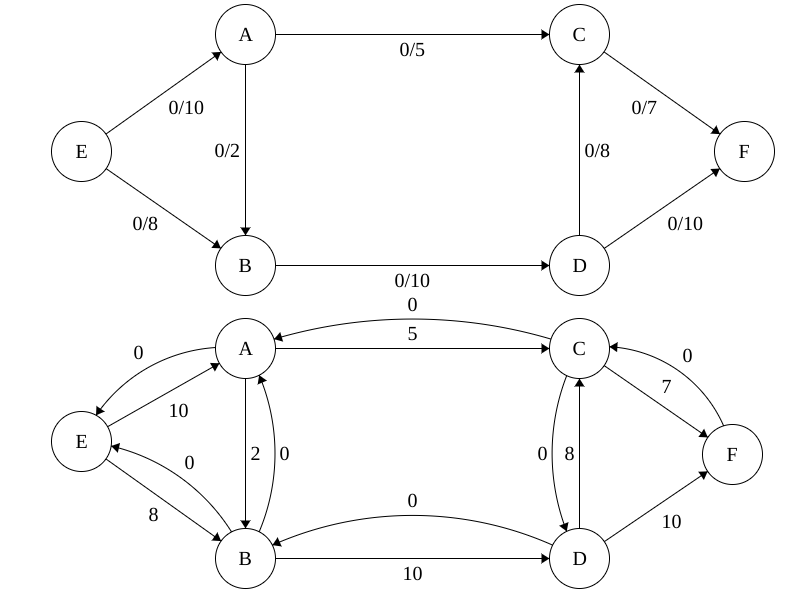
Part 1: Constructing the Network Flow
To calculate the flow of a network using the algorithm discussed in lab, you need to have both a flow and residual graph. The goal of your constructor is to build the residual and flow graphs from the provided graph.
Part 2: Calculating the Overall Capacity of a Path in a Network
Next, we need to calculate the net capacity of a provided path. To do so, simply find the minimum weight among the edges in the path in the residual graph by iterating through the vertices in the path vector.
Part 3: Calculate the Flow in a Network
Now, we will take the function made in Part 2, pathCapacity() and use it to help us calculate the total flow of our graph network. Here is a breakdown of the algorithm in its fundamental steps.
- Keep looping until no more valid augmenting paths can be found.
- In the loop, get the capacity of the path found using
pathCapacity() - Using that capacity, you will update three paths:
- Add the capacity to the edges in the corresponding path in the flow graph. Note that this path may go in the opposite direction of the edge in your graph. In that case, reverse the vertices and subtract the capcity from the edge in the flow graph
- Subtract the capacity from the forward edges in the residual graph.
- Add the capacity to the reverse edges in the residual graph.
The algorithm is finished when no more paths with nonzero capacity can be found from the source node to the sink node.
Let’s Test Out Network Flow
A main.cpp is provided that lets you simulate a small network flow example:
./lab_flow
After testing with this binary, be sure to use our full set of test cases for this lab.
./test
Grading Information
The following files are used for grading this lab:
NetworkFlow.hNetworkFlow.cpp
If you modify any other files, they will not be grabbed for grading and you may
end up with an “unfortunate zero.” (You may modify NetworkFlow.h, but it is
possible to solve the problem without doing so.)